Approximate string matching
Encyclopedia
In computing
, approximate string matching (often colloquially referred to as fuzzy string searching) is the technique of finding strings that match a pattern
approximately (rather than exactly). The problem of approximate string matching is typically divided into two sub-problems: finding approximate substring
matches inside a given string and finding dictionary strings that match the pattern approximately.
between the string and the pattern. The usual primitive operations are:
These three operations may be generalized as forms of substitution by adding a NULL character (here symbolized by λ) wherever a character has been deleted or inserted:
Some approximate matchers also treat transposition, in which the positions of two letters in the string are swapped, to be a primitive operation. Changing cost to cots is an example of a transposition.
Different approximate matchers impose different constraints. Some matchers use a single global unweighted cost, that is, the total number of primitive operations necessary to convert the match to the pattern. For example, if the pattern is coil, foil differs by one substitution, coils by one insertion, oil by one deletion, and foal by two substitutions. If all operations count as a single unit of cost and the limit is set to one, foil, coils, and oil will count as matches while foal will not.
Other matchers specify the number of operations of each type separately, while still others set a total cost but allow different weights to be assigned to different operations. Some matchers permit separate assignments of limits and weights to individual groups in the pattern.
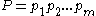and a text string 
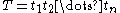, find a substring 
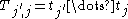in T, which, of all substrings of T, has the smallest edit distance to the pattern P.
A brute-force approach would be to compute the edit distance to P for all substrings of T, and then choose the substring with the minimum distance. However, this algorithm would have the running time O
(n3 m)
A better solution, which was proposed by Sellers , relies on the dynamic programming
. It uses an alternative formulation of the problem: for each position j in the text T and each position i in the pattern P, compute the minimum edit distance between the i first characters of the pattern,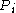
, and any substring 
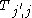of T that ends at position j.
For each position j in the text T, and each position i in the pattern P, go through all substrings of T ending at position j, and determine which one of them has the minimal
edit distance to the i first characters of the pattern P. Write this minimal distance as E(i, j). After computing E(i, j) for all i and j, we can easily find a solution to the original problem: it is the substring for which E(m, j) is minimal (m being the length of the pattern P.)
Computing E(m, j) is very similar to computing the edit distance between two strings. In fact, we can use the Levenshtein distance computing algorithm for E(m, j), the only difference being that we must initialize the first row with zeros, and save the path of computation, that is, whether we used E(i − 1,j), E(i,j − 1) or E(i − 1,j − 1) in computing E(i, j).
In the array containing the E(x, y) values, we then choose the minimal value in the last row, let it be E(x2, y2), and follow the path of computation backwards, back to the row number 0. If the field we arrived at was E(x1, 0), then T[x1 + 1] ... T[y2] is a substring of T with the minimal edit distance to the pattern P.
Computing the E(x, y) array takes O
(mn) time with the dynamic programming algorithm, while the backwards-working phase takes O
(n + m) time.
but solve different problems. Sellers' algorithm searches approximately for a substring in a text while the algorithm of Wagner and Fisher calculates Levenshtein distance
, being appropriate for dictionary fuzzy search only.
On-line searching techniques have been repeatedly improved. Perhaps the most
famous improvement is the bitap algorithm
(also known as the shift-or and shift-and algorithm), which is very efficient for relatively short pattern strings. The Bitap algorithm is the heart of the Unix
searching utility
agrep
. A review of on-line searching algorithms was done by G. Navarro.
Although very fast on-line techniques exist, their
performance on large data is unacceptable.
Text preprocessing or indexing
makes searching dramatically faster.
Today, a variety of indexing algorithms have been presented. Among them are suffix tree
s, metric tree
s and n-gram
methods.
A detailed survey of indexing techniques that allows one to find an arbitrary substring in a text is given by Navarro et al.. A computational survey of dictionary methods (i.e., methods that permit finding all dictionary words that approximately match a search pattern) is given by Boytsov .
sequences has become an important application. Approximate matching is also used to identify pieces of music from small snatches and in spam filtering.
Computing
Computing is usually defined as the activity of using and improving computer hardware and software. It is the computer-specific part of information technology...
, approximate string matching (often colloquially referred to as fuzzy string searching) is the technique of finding strings that match a pattern
Pattern
A pattern, from the French patron, is a type of theme of recurring events or objects, sometimes referred to as elements of a set of objects.These elements repeat in a predictable manner...
approximately (rather than exactly). The problem of approximate string matching is typically divided into two sub-problems: finding approximate substring
Substring
A subsequence, substring, prefix or suffix of a string is a subset of the symbols in a string, where the order of the elements is preserved...
matches inside a given string and finding dictionary strings that match the pattern approximately.
Overview
The closeness of a match is measured in terms of the number of primitive operations necessary to convert the string into an exact match. This number is called the edit distanceEdit distance
In information theory and computer science, the edit distance between two strings of characters generally refers to the Levenshtein distance. However, according to Nico Jacobs, “The term ‘edit distance’ is sometimes used to refer to the distance in which insertions and deletions have equal cost and...
between the string and the pattern. The usual primitive operations are:
- insertion: cot → coat
- deletion: coat → cot
- substitution: coat → cost
These three operations may be generalized as forms of substitution by adding a NULL character (here symbolized by λ) wherever a character has been deleted or inserted:
- insertion: coλt → coat
- deletion: coat → coλt
- substitution: coat → cost
Some approximate matchers also treat transposition, in which the positions of two letters in the string are swapped, to be a primitive operation. Changing cost to cots is an example of a transposition.
Different approximate matchers impose different constraints. Some matchers use a single global unweighted cost, that is, the total number of primitive operations necessary to convert the match to the pattern. For example, if the pattern is coil, foil differs by one substitution, coils by one insertion, oil by one deletion, and foal by two substitutions. If all operations count as a single unit of cost and the limit is set to one, foil, coils, and oil will count as matches while foal will not.
Other matchers specify the number of operations of each type separately, while still others set a total cost but allow different weights to be assigned to different operations. Some matchers permit separate assignments of limits and weights to individual groups in the pattern.
Problem formulation and algorithms
One possible definition of the approximate string matching problem is the following: Given a pattern string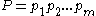 and a text string 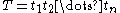, find a substring 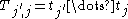in T, which, of all substrings of T, has the smallest edit distance to the pattern P.A brute-force approach would be to compute the edit distance to P for all substrings of T, and then choose the substring with the minimum distance. However, this algorithm would have the running time O
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
(n3 m)
A better solution, which was proposed by Sellers , relies on the dynamic programming
Dynamic programming
In mathematics and computer science, dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It is applicable to problems exhibiting the properties of overlapping subproblems which are only slightly smaller and optimal substructure...
. It uses an alternative formulation of the problem: for each position j in the text T and each position i in the pattern P, compute the minimum edit distance between the i first characters of the pattern,
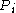, and any substring 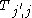of T that ends at position j.For each position j in the text T, and each position i in the pattern P, go through all substrings of T ending at position j, and determine which one of them has the minimal
edit distance to the i first characters of the pattern P. Write this minimal distance as E(i, j). After computing E(i, j) for all i and j, we can easily find a solution to the original problem: it is the substring for which E(m, j) is minimal (m being the length of the pattern P.)
Computing E(m, j) is very similar to computing the edit distance between two strings. In fact, we can use the Levenshtein distance computing algorithm for E(m, j), the only difference being that we must initialize the first row with zeros, and save the path of computation, that is, whether we used E(i − 1,j), E(i,j − 1) or E(i − 1,j − 1) in computing E(i, j).
In the array containing the E(x, y) values, we then choose the minimal value in the last row, let it be E(x2, y2), and follow the path of computation backwards, back to the row number 0. If the field we arrived at was E(x1, 0), then T[x1 + 1] ... T[y2] is a substring of T with the minimal edit distance to the pattern P.
Computing the E(x, y) array takes O
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
(mn) time with the dynamic programming algorithm, while the backwards-working phase takes O
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
(n + m) time.
On-line versus off-line
Traditionally, approximate string matching algorithms are classified into two categories: on-line and off-line. With on-line algorithms the pattern can be preprocessed before searching but the text cannot. In other words, on-line techniques do searching without an index. Early algorithms for on-line approximate matching were suggested by Wagner and Fisher and by Sellers. Both algorithms are based on dynamic programmingDynamic programming
In mathematics and computer science, dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It is applicable to problems exhibiting the properties of overlapping subproblems which are only slightly smaller and optimal substructure...
but solve different problems. Sellers' algorithm searches approximately for a substring in a text while the algorithm of Wagner and Fisher calculates Levenshtein distance
Levenshtein distance
In information theory and computer science, the Levenshtein distance is a string metric for measuring the amount of difference between two sequences...
, being appropriate for dictionary fuzzy search only.
On-line searching techniques have been repeatedly improved. Perhaps the most
famous improvement is the bitap algorithm
Bitap algorithm
The bitap algorithm is an approximate string matching algorithm...
(also known as the shift-or and shift-and algorithm), which is very efficient for relatively short pattern strings. The Bitap algorithm is the heart of the Unix
Unix
Unix is a multitasking, multi-user computer operating system originally developed in 1969 by a group of AT&T employees at Bell Labs, including Ken Thompson, Dennis Ritchie, Brian Kernighan, Douglas McIlroy, and Joe Ossanna...
searching utility
Programming tool
A programming tool or software development tool is a program or application that software developers use to create, debug, maintain, or otherwise support other programs and applications...
agrep
Agrep
agrep is a proprietary fuzzy string searching program, developed by Udi Manber and Sun Wu between 1988 and 1991, for use with the Unix operating system...
. A review of on-line searching algorithms was done by G. Navarro.
Although very fast on-line techniques exist, their
performance on large data is unacceptable.
Text preprocessing or indexing
Index (search engine)
Search engine indexing collects, parses, and stores data to facilitate fast and accurate information retrieval. Index design incorporates interdisciplinary concepts from linguistics, cognitive psychology, mathematics, informatics, physics, and computer science...
makes searching dramatically faster.
Today, a variety of indexing algorithms have been presented. Among them are suffix tree
Suffix tree
In computer science, a suffix tree is a data structure that presents the suffixes of a given string in a way that allows for a particularly fast implementation of many important string operations.The suffix tree for a string S is a tree whose edges are labeled with strings, such that each suffix...
s, metric tree
Metric tree
A metric tree is any tree data structure specialized to index data in metric spaces. Metric trees exploit properties of metric spaces such as the triangle inequality to make accesses to the data more efficient...
s and n-gram
N-gram
In the fields of computational linguistics and probability, an n-gram is a contiguous sequence of n items from a given sequence of text or speech. The items in question can be phonemes, syllables, letters, words or base pairs according to the application...
methods.
A detailed survey of indexing techniques that allows one to find an arbitrary substring in a text is given by Navarro et al.. A computational survey of dictionary methods (i.e., methods that permit finding all dictionary words that approximately match a search pattern) is given by Boytsov .
Applications
The most common application of approximate matchers until recently has been spell checking. With the availability of large amounts of DNA data, matching of nucleotideNucleotide
Nucleotides are molecules that, when joined together, make up the structural units of RNA and DNA. In addition, nucleotides participate in cellular signaling , and are incorporated into important cofactors of enzymatic reactions...
sequences has become an important application. Approximate matching is also used to identify pieces of music from small snatches and in spam filtering.
See also
- String metricString metricIn mathematics, string metrics are a class of metric that measure similarity or dissimilarity between two text strings for approximate string matching or comparison and in fuzzy string searching. For example the strings "Sam" and "Samuel" can be considered to be similar...
- Needleman–Wunsch algorithmNeedleman–Wunsch algorithmThe Needleman–Wunsch algorithm performs a global alignment on two sequences . It is commonly used in bioinformatics to align protein or nucleotide sequences. The algorithm was published in 1970 by Saul B. Needleman and Christian D...
- Smith–Waterman algorithm
- Levenshtein distanceLevenshtein distanceIn information theory and computer science, the Levenshtein distance is a string metric for measuring the amount of difference between two sequences...
- MetaphoneMetaphoneMetaphone is a phonetic algorithm, an algorithm published in 1990 for indexing words by their English pronunciation. It fundamentally improves on the Soundex algorithm by using information about variations and inconsistencies in English spelling and pronunciation to produce a more accurate...
- SoundexSoundexSoundex is a phonetic algorithm for indexing names by sound, as pronounced in English. The goal is for homophones to be encoded to the same representation so that they can be matched despite minor differences in spelling. The algorithm mainly encodes consonants; a vowel will not be encoded unless...
- AgrepAgrepagrep is a proprietary fuzzy string searching program, developed by Udi Manber and Sun Wu between 1988 and 1991, for use with the Unix operating system...
- Approximate matching with addition of regular expressions ability
- Regular expressions for non-fuzzy (exact) matching
- fuzzystrmatch module in PostgreSQLPostgreSQLPostgreSQL, often simply Postgres, is an object-relational database management system available for many platforms including Linux, FreeBSD, Solaris, MS Windows and Mac OS X. It is released under the PostgreSQL License, which is an MIT-style license, and is thus free and open source software...
- An extension of Ukkonen's enhanced dynamic programming ASM algorithm, Hal Berghel, University of Arkansas, and David Roach, Acxiom Corporation
- Flamingo Project
- Plagiarism detectionPlagiarism detectionPlagiarism detection is the process of locating instances of plagiarism within a work or document. The widespread use of computers and the advent of the Internet has made it easier to plagiarize the work of others. Most cases of plagiarism are found in academia, where documents are typically essays...