Needleman–Wunsch algorithm
Encyclopedia
The Needleman–Wunsch algorithm performs a global alignment on two sequences (called A and B here). It is commonly used in bioinformatics
to align protein
or nucleotide
sequences. The algorithm was published in 1970 by Saul B. Needleman and Christian D. Wunsch.
The Needleman–Wunsch algorithm
is an example of dynamic programming
, and was the first application of dynamic programming to biological sequence comparison.
. Here,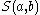
is the similarity of characters a and b. It uses a linear gap penalty
, here called d.
For example, if the similarity matrix were
then the alignment:
AGACTAGTTAC
CGA‒‒‒GACGT
with a gap penalty of -5, would have the following score:
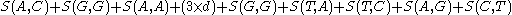
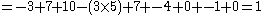
To find the alignment with the highest score, a two-dimensional array (or matrix
) F is allocated. The entry in row i and column j is denoted here by
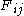. There is one column for each character in sequence A, and one row for each character in sequence B. Thus, if we are aligning sequences of sizes n and m, the amount of memory used is in 
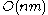. (Hirschberg's algorithm
can compute an optimal alignment in
space, roughly doubling the running time.)
As the algorithm progresses, the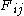
will be assigned to be the optimal score for the alignment of the first 
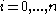characters in A and the first 
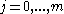characters in B. The principle of optimality is then applied as follows.
Basis:
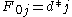
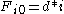
Recursion, based on the principle of optimality:
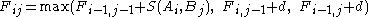
The pseudo-code for the algorithm to compute the F matrix therefore looks like this:
for i=0 to length(A)
F(i,0) ← d*i
for j=0 to length(B)
F(0,j) ← d*j
for i=1 to length(A)
for j=1 to length(B)
{
Match ← F(i-1,j-1) + S(Ai, Bj)
Delete ← F(i-1, j) + d
Insert ← F(i, j-1) + d
F(i,j) ← max(Match, Insert, Delete)
}
Once the F matrix is computed, the entry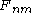
gives the maximum score among all possible alignments. To compute an alignment that actually gives this score, you start from the bottom right cell, and compare the value with the three possible sources (Match, Insert, and Delete above) to see which it came from. If Match, then 
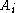and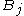 
are aligned, if Delete, then 
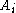is aligned with a gap, and if Insert, then 
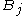is aligned with a gap. (In general, more than one choices may have the same value, leading to alternative optimal alignments.)
AlignmentA ← ""
AlignmentB ← ""
i ← length(A)
j ← length(B)
while (i > 0 and j > 0)
{
Score ← F(i,j)
ScoreDiag ← F(i - 1, j - 1)
ScoreUp ← F(i, j - 1)
ScoreLeft ← F(i - 1, j)
if (Score ScoreDiag + S(Ai, Bj))
ScoreLeft + d)
{
AlignmentA ← Ai + AlignmentA
AlignmentB ← "-" + AlignmentB
i ← i - 1
}
otherwise (Score ScoreUp + d)
{
AlignmentA ← "-" + AlignmentA
AlignmentB ← Bj + AlignmentB
j ← j - 1
}
}
while (i > 0)
{
AlignmentA ← Ai + AlignmentA
AlignmentB ← "-" + AlignmentB
i ← i - 1
}
while (j > 0)
{
AlignmentA ← "-" + AlignmentA
AlignmentB ← Bj + AlignmentB
j ← j - 1
}
Historical notes
Needleman and Wunsch describe their algorithm explicitly for the case when the alignment is penalized solely by the matches and mismatches, and gaps have no penalty (d=0). The original publication from 1970 suggests the recursion
.
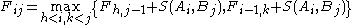The corresponding dynamic programming algorithm takes cubic time. The paper also points out that the recursion can accommodate arbitrary gap penalization formulas:
A better dynamic programming algorithm with quadratic running time for the same problem (no gap penalty) was first introduced by David Sankoff in 1972.
Similar quadratic-time algorithms were discovered independently
by T. K. Vintsyuk in 1968 for speech processing
("time warping"
), and by Robert A. Wagner and Michael J. Fischer
in 1974 for string matching.
Needleman and Wunsch formulated their problem in terms of maximizing similarity. Another possibility is to minimize the edit distance
between sequences, introduced by Vladimir Levenshtein
. Peter H. Sellers showed in 1974 that the two problems are equivalent.
In modern terminology, "Needleman-Wunsch" refers to
a global alignment algorithm that takes quadratic time for a linear or affine gap penalty.
External links
See also
Bioinformatics
Bioinformatics is the application of computer science and information technology to the field of biology and medicine. Bioinformatics deals with algorithms, databases and information systems, web technologies, artificial intelligence and soft computing, information and computation theory, software...
to align protein
Protein
Proteins are biochemical compounds consisting of one or more polypeptides typically folded into a globular or fibrous form, facilitating a biological function. A polypeptide is a single linear polymer chain of amino acids bonded together by peptide bonds between the carboxyl and amino groups of...
or nucleotide
Nucleotide
Nucleotides are molecules that, when joined together, make up the structural units of RNA and DNA. In addition, nucleotides participate in cellular signaling , and are incorporated into important cofactors of enzymatic reactions...
sequences. The algorithm was published in 1970 by Saul B. Needleman and Christian D. Wunsch.
The Needleman–Wunsch algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
is an example of dynamic programming
Dynamic programming
In mathematics and computer science, dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It is applicable to problems exhibiting the properties of overlapping subproblems which are only slightly smaller and optimal substructure...
, and was the first application of dynamic programming to biological sequence comparison.
A modern presentation
Scores for aligned characters are specified by a similarity matrixSimilarity matrix
A similarity matrix is a matrix of scores which express the similarity between two data points. Similarity matrices are strongly related to their counterparts, distance matrices and substitution matrices.-Use in sequence alignment:...
. Here,
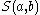is the similarity of characters a and b. It uses a linear gap penaltyGap penalty
Gap penalties are used during sequence alignment. Gap penalties contribute to the overall score of alignments, and therefore, the size of the gap penalty relative to the entries in the similarity matrix affects the alignment that is finally selected...
, here called d.
For example, if the similarity matrix were
| A | G | C | T | |
|---|---|---|---|---|
| A | 10 | -1 | -3 | -4 |
| G | -1 | 7 | -5 | -3 |
| C | -3 | -5 | 9 | 0 |
| T | -4 | -3 | 0 | 8 |
then the alignment:
AGACTAGTTAC
CGA‒‒‒GACGT
with a gap penalty of -5, would have the following score:
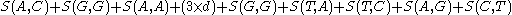
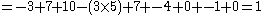
To find the alignment with the highest score, a two-dimensional array (or matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
) F is allocated. The entry in row i and column j is denoted here by
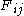. There is one column for each character in sequence A, and one row for each character in sequence B. Thus, if we are aligning sequences of sizes n and m, the amount of memory used is in 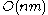. (Hirschberg's algorithmHirschberg's algorithm
Hirschberg's algorithm, named after its inventor, Dan Hirschberg, is a dynamic programming algorithm that finds the least cost sequence alignment between two strings, where cost is measured as Levenshtein distance, defined to be the sum of the costs of insertions, replacements, deletions, and null...
can compute an optimal alignment in
space, roughly doubling the running time.)As the algorithm progresses, the
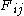will be assigned to be the optimal score for the alignment of the first 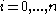characters in A and the first 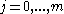characters in B. The principle of optimality is then applied as follows.Basis:
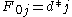
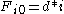
Recursion, based on the principle of optimality:
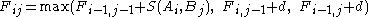
The pseudo-code for the algorithm to compute the F matrix therefore looks like this:
for i=0 to length(A)
F(i,0) ← d*i
for j=0 to length(B)
F(0,j) ← d*j
for i=1 to length(A)
for j=1 to length(B)
{
Match ← F(i-1,j-1) + S(Ai, Bj)
Delete ← F(i-1, j) + d
Insert ← F(i, j-1) + d
F(i,j) ← max(Match, Insert, Delete)
}
Once the F matrix is computed, the entry
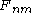gives the maximum score among all possible alignments. To compute an alignment that actually gives this score, you start from the bottom right cell, and compare the value with the three possible sources (Match, Insert, and Delete above) to see which it came from. If Match, then 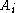and 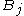are aligned, if Delete, then 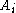is aligned with a gap, and if Insert, then 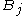is aligned with a gap. (In general, more than one choices may have the same value, leading to alternative optimal alignments.)AlignmentA ← ""
AlignmentB ← ""
i ← length(A)
j ← length(B)
while (i > 0 and j > 0)
{
Score ← F(i,j)
ScoreDiag ← F(i - 1, j - 1)
ScoreUp ← F(i, j - 1)
ScoreLeft ← F(i - 1, j)
if (Score
ScoreDiag + S(Ai, Bj))
{
AlignmentA ← Ai + AlignmentA
AlignmentB ← Bj + AlignmentB
i ← i - 1
j ← j - 1
}
else if (Score
ScoreLeft + d){
AlignmentA ← Ai + AlignmentA
AlignmentB ← "-" + AlignmentB
i ← i - 1
}
otherwise (Score ScoreUp + d)
{
AlignmentA ← "-" + AlignmentA
AlignmentB ← Bj + AlignmentB
j ← j - 1
}
}
while (i > 0)
{
AlignmentA ← Ai + AlignmentA
AlignmentB ← "-" + AlignmentB
i ← i - 1
}
while (j > 0)
{
AlignmentA ← "-" + AlignmentA
AlignmentB ← Bj + AlignmentB
j ← j - 1
}
Historical notes
Needleman and Wunsch describe their algorithm explicitly for the case when the alignment is penalized solely by the matches and mismatches, and gaps have no penalty (d=0). The original publication from 1970 suggests the recursion
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
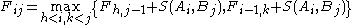.The corresponding dynamic programming algorithm takes cubic time. The paper also points out that the recursion can accommodate arbitrary gap penalization formulas:
A penalty factor, a number subtracted for every gap made, may be assessed as a barrier to allowing the gap. The penalty factor could be a function of the size and/or direction of the gap. [page 444]
A better dynamic programming algorithm with quadratic running time for the same problem (no gap penalty) was first introduced by David Sankoff in 1972.
Similar quadratic-time algorithms were discovered independently
by T. K. Vintsyuk in 1968 for speech processing
("time warping"
Dynamic time warping
Dynamic time warping is an algorithm for measuring similarity between two sequences which may vary in time or speed. For instance, similarities in walking patterns would be detected, even if in one video the person was walking slowly and if in another he or she were walking more quickly, or even...
), and by Robert A. Wagner and Michael J. Fischer
Michael J. Fischer
Michael John Fischer is a computer scientist who works in the fields of distributed computing, parallel computing, cryptography, algorithms and data structures, and computational complexity.-Career:...
in 1974 for string matching.
Needleman and Wunsch formulated their problem in terms of maximizing similarity. Another possibility is to minimize the edit distance
Levenshtein distance
In information theory and computer science, the Levenshtein distance is a string metric for measuring the amount of difference between two sequences...
between sequences, introduced by Vladimir Levenshtein
Vladimir Levenshtein
Vladimir Iosifovich Levenshtein is a Russian scientist who did research in information theory and error-correcting codes. Among other contributions, he is known for the Levenshtein distance algorithm, which he developed in 1965....
. Peter H. Sellers showed in 1974 that the two problems are equivalent.
In modern terminology, "Needleman-Wunsch" refers to
a global alignment algorithm that takes quadratic time for a linear or affine gap penalty.
External links
- NW-align: A protein sequence-to-sequence alignment program by Needleman-Wunsch algorithm (online server & source code)
- Needleman-Wunsch Algorithm as Ruby Code
- Java Implementation of the Needleman-Wunsch Algorithm
- B.A.B.A. — an applet (with source) which visually explains the algorithm.
- A clear explanation of NW and its applications to sequence alignment
- Sequence Alignment Techniques at Technology Blog
- OPAL JavaScript implementation of algorithms: Needleman-Wunsch, Needleman-Wunsch-Sellers and Smith-Waterman
- Biostrings R package implementing Needleman-Wunsch algorithm among others
See also
- Smith-Waterman algorithm
- BLASTBLASTIn bioinformatics, Basic Local Alignment Search Tool, or BLAST, is an algorithm for comparing primary biological sequence information, such as the amino-acid sequences of different proteins or the nucleotides of DNA sequences...
- Levenshtein distanceLevenshtein distanceIn information theory and computer science, the Levenshtein distance is a string metric for measuring the amount of difference between two sequences...
- Dynamic time warpingDynamic time warpingDynamic time warping is an algorithm for measuring similarity between two sequences which may vary in time or speed. For instance, similarities in walking patterns would be detected, even if in one video the person was walking slowly and if in another he or she were walking more quickly, or even...