
Appert topology
Encyclopedia
In general topology
, a branch of mathematics, the Appert topology, named for , is an example of a topology
on the set } of positive integers
. To give Z+ a topology means to say which subset
s of Z+ are open
in a manner that satisfies certain axioms:
In the Appert topology, the open sets are those that do not contain 1, and those that asymptotically contain almost every positive integer.

In Appert's topology, a set S is defined to be open if either it does not contain 1 or N(n,S)/n tends towards 1 as n tends towards infinity: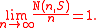
The empty set is an open set in this topology because ∅ is a set that does not contain 1, and the whole set Z+ is also open in this topology since
meaning that for all n.
topology that arises from giving the set of integers greater than one the discrete topology, and then taking the point 1 as the point at infinity in a one point compactification of the space. The Fort space is a refinement of the Appert topology.
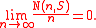
As a result, Z+ is a completely normal space (and thus also Hausdorff
), for suppose that A and B are disjoint closed sets. If did not contain 1, then A and B would also be open and thus completely separated. On the other hand, if A contains 1 then B is open and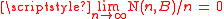 , so that Z+−B is an open neighborhood of A disjoint from B.
, so that Z+−B is an open neighborhood of A disjoint from B.
A subset of Z+ is compact
in the Appert topology if and only if it is finite. In particular, Z+ is not locally compact
, since there is no compact neighborhood of 1. Moreover, Z+ is not countably compact.
General topology
In mathematics, general topology or point-set topology is the branch of topology which studies properties of topological spaces and structures defined on them...
, a branch of mathematics, the Appert topology, named for , is an example of a topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
on the set } of positive integers
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
. To give Z+ a topology means to say which subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of Z+ are open
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
in a manner that satisfies certain axioms:
- The union of open sets is an open set.
- The finite intersection of open sets is an open set.
- Z+ and the empty setEmpty setIn mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
∅ are open sets.
In the Appert topology, the open sets are those that do not contain 1, and those that asymptotically contain almost every positive integer.
Construction
Let S be a subset of Z+, and let denote the number of elements of S which are less than or equal to n:
In Appert's topology, a set S is defined to be open if either it does not contain 1 or N(n,S)/n tends towards 1 as n tends towards infinity:
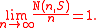
The empty set is an open set in this topology because ∅ is a set that does not contain 1, and the whole set Z+ is also open in this topology since

meaning that for all n.
Related topologies
The Appert topology is closely related to the Fort spaceFort space
In mathematics, Fort space, named after M. K. Fort, Jr., is an example in the theory of topological spaces.Let X be an infinite set of points, of which P is one...
topology that arises from giving the set of integers greater than one the discrete topology, and then taking the point 1 as the point at infinity in a one point compactification of the space. The Fort space is a refinement of the Appert topology.
Properties
The closed subsets of Z+, equipped with the Appert topology, are the subsets S that either contain 1 or for which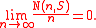
As a result, Z+ is a completely normal space (and thus also Hausdorff
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
), for suppose that A and B are disjoint closed sets. If did not contain 1, then A and B would also be open and thus completely separated. On the other hand, if A contains 1 then B is open and
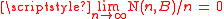 , so that Z+−B is an open neighborhood of A disjoint from B.
, so that Z+−B is an open neighborhood of A disjoint from B.A subset of Z+ is compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
in the Appert topology if and only if it is finite. In particular, Z+ is not locally compact
Locally compact space
In topology and related branches of mathematics, a topological space is called locally compact if, roughly speaking, each small portion of the space looks like a small portion of a compact space.-Formal definition:...
, since there is no compact neighborhood of 1. Moreover, Z+ is not countably compact.

