Appell's equation of motion
Encyclopedia
In classical mechanics
, Appell's equation of motion is an alternative general formulation of classical mechanics
described by Paul Émile Appell
in 1900
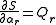
Here,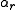
is an arbitrary generalized acceleration and Qr is its corresponding generalized force; that is, the work done is given by
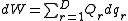
where the index r runs over the D generalized coordinates qr, which usually correspond to the degrees of freedom
of the system. The function S is defined as the mass-weighted sum of the particle acceleration
s squared, having the dimension of a generalised force for a generalised acceleration:
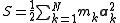
where the index k runs over the N particles. Although fully equivalent to the other formulations of classical mechanics such as Newton's second law
and the principle of least action
, Appell's equation of motion may be more convenient in some cases, particularly when constraints are involved. Appell’s formulation can be viewed as a variation of Gauss' principle of least constraint.
Consider a rigid body of N particles joined by rigid rods. The rotation of the body may be described by an angular velocity
vector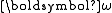
, and the corresponding angular acceleration vector
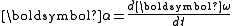
The generalized force for a rotation is the torque N, since the work done for an infinitesimal rotation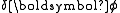
is 
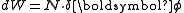. The velocity of the kth particle is given by
where rk is the particle's position in Cartesian coordinates; its corresponding acceleration is
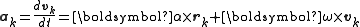
Therefore, the function S may be written as
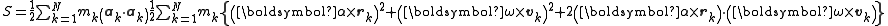
Setting the derivative of S with respect to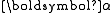
equal to the torque yields Euler's equations
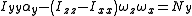
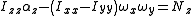
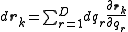
Taking two derivatives with respect to time yields an equivalent equation for the accelerations
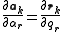
The work done by an infinitesimal change dqr in the generalized coordinates is
Substituting the formula for drk and swapping the order of the two summations yields the formulae
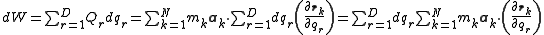
Therefore, the generalized forces are
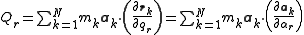
This equals the derivative of S with respect to the generalized accelerations
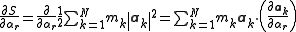
yielding Appell’s equation of motion
.
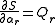
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
, Appell's equation of motion is an alternative general formulation of classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
described by Paul Émile Appell
Paul Émile Appell
Paul Appell , also known as Paul Émile Appel, was a French mathematician and Rector of the University of Paris...
in 1900
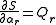
Here,
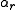is an arbitrary generalized acceleration and Qr is its corresponding generalized force; that is, the work done is given by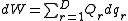where the index r runs over the D generalized coordinates qr, which usually correspond to the degrees of freedom
Degrees of freedom (physics and chemistry)
A degree of freedom is an independent physical parameter, often called a dimension, in the formal description of the state of a physical system...
of the system. The function S is defined as the mass-weighted sum of the particle acceleration
Acceleration
In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
s squared, having the dimension of a generalised force for a generalised acceleration:
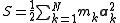
where the index k runs over the N particles. Although fully equivalent to the other formulations of classical mechanics such as Newton's second law
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
and the principle of least action
Principle of least action
In physics, the principle of least action – or, more accurately, the principle of stationary action – is a variational principle that, when applied to the action of a mechanical system, can be used to obtain the equations of motion for that system...
, Appell's equation of motion may be more convenient in some cases, particularly when constraints are involved. Appell’s formulation can be viewed as a variation of Gauss' principle of least constraint.
Example: Euler's equations
Euler's equations provide an excellent illustration of Appell's formulation.Consider a rigid body of N particles joined by rigid rods. The rotation of the body may be described by an angular velocity
Angular velocity
In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...
vector
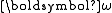, and the corresponding angular acceleration vector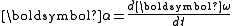The generalized force for a rotation is the torque N, since the work done for an infinitesimal rotation
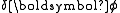is 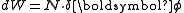. The velocity of the kth particle is given bywhere rk is the particle's position in Cartesian coordinates; its corresponding acceleration is
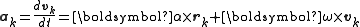
Therefore, the function S may be written as
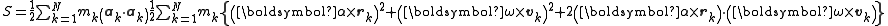
Setting the derivative of S with respect to
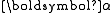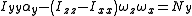
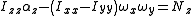
equal to the torque yields Euler's equationsDerivation
The change in the particle positions rk for an infinitesimal change in the D generalized coordinates is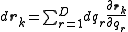Taking two derivatives with respect to time yields an equivalent equation for the accelerations
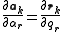
The work done by an infinitesimal change dqr in the generalized coordinates is
Substituting the formula for drk and swapping the order of the two summations yields the formulae
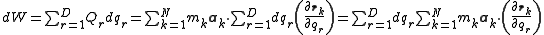
Therefore, the generalized forces are
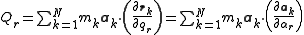
This equals the derivative of S with respect to the generalized accelerations
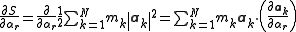
yielding Appell’s equation of motion
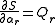
Further reading
Connection of Appell's formulation with the principle of least actionPrinciple of least action
In physics, the principle of least action – or, more accurately, the principle of stationary action – is a variational principle that, when applied to the action of a mechanical system, can be used to obtain the equations of motion for that system...
.