
Apothem
Encyclopedia
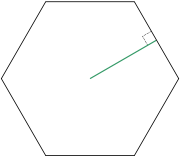
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
is a line segment from the center to the midpoint of one of its sides. Equivalently, it is the line drawn from the center of the polygon that is perpendicular to one of its sides. The word "apothem" can also refer to the length of that line segment. Regular polygons are the only polygons that have apothems. Because of this, all the apothems in a polygon will be congruent
Congruence (geometry)
In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...
and have the same length.
For a regular pyramid
Pyramid (geometry)
In geometry, a pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex. Each base edge and apex form a triangle. It is a conic solid with polygonal base....
, which is a pyramid whose base is a regular polygon, the apothem is the slant height of a lateral face; that is, the shortest distance from apex to base on a given face. For a truncated regular pyramid (a regular pyramid with some of its peak removed by a plane parallel to the base), the apothem is the height of a trapezoidal lateral face. http://www.bymath.com/studyguide/geo/sec/geo15.htm
For a triangle (necessarily equilateral), the apothem is equivalent to the line segment from the midpoint of a side to any of the triangle's centers, since an equilateral triangle's centers coincide as a consequence of the definition.
Properties of apothems
The apothem a can be used to find the area of any regular n-sided polygon of side length s according to the following formula, which also states that the area is equal to the apothem multiplied by half the perimeter since ns = p.
This formula can be derived by partitioning the n-sided polygon into n congruent
Congruence (geometry)
In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...
isosceles triangles, and then noting that the apothem is the height of each triangle, and that the area of a triangle equals half the base times the height.
An apothem of a regular polygon will always be a radius of the inscribe
Inscribe
right|thumb|An inscribed triangle of a circleIn geometry, an inscribed planar shape or solid is one that is enclosed by and "fits snugly" inside another geometric shape or solid. To say that "Figure F is inscribed in figure G" means precisely the same thing as "figure G is circumscribed about...
d circle. It is also the minimum distance between any side of the polygon and its center.
This property can also be used to easily derive the formula for the area of a circle, because as the number of sides approaches infinity, the regular polygon's area approaches the area of the inscribed circle of radius r = a.

Finding the apothem
The apothem of a regular polygon can be found multiple ways, of which two are described here.The apothem a of a regular n-sided polygon with side length s, or circumradius R, can be found using the following formula:

The apothem can also be found by

Both formulas can still be used even if only the perimeter p and the number of sides n are known because

External links
- Apothem of a regular polygon With interactive animation
- Apothem of pyramid or truncated pyramid
- Sagitta, Apothem, and Chord by Ed Pegg, Jr.Ed Pegg, Jr.Ed Pegg, Jr. is an expert on mathematical puzzles and is a self-described recreational mathematician. He creates puzzles for the Mathematical Association of America online at Ed Pegg, Jr.'s Math Games. His puzzles have also been used by Will Shortz on the puzzle segment of NPR's Weekend Edition...
, The Wolfram Demonstrations Project.

