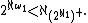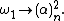András Hajnal
Encyclopedia
András Hajnal is an emeritus professor of mathematics at Rutgers University
and a member of the Hungarian Academy of Sciences
known for his work in set theory
and combinatorics
.
.
He received his university diploma (M.Sc. degree) in 1953 from the Eötvös Loránd University, his Candidate of Mathematical Science degree (roughly equivalent to Ph.D.) in 1957, under the supervision of László Kalmár
, and his Doctor of Mathematical Science degree in 1962. From 1956 to 1995 he was a faculty member at the Eötvös Loránd University; in 1994, he moved to Rutgers University to become the director of DIMACS
, and he remained there as a professor until his retirement in 2004. He became a member of the Hungarian Academy of Sciences in 1982, and directed its mathematical institute
from 1982 to 1992. He was general secretary of the János Bolyai Mathematical Society
from 1980 to 1990, and president of the society from 1990 to 1994. Since 1981, he has been an advisory editor of the journal Combinatorica
.
In all his life, Hajnal has been an avid chess
player.
Hajnal is the father of Peter Hajnal, the co-dean of the European College of Liberal Arts
.
, he has the second largest number of joint papers, 56.
With Peter Hamburger, he wrote a textbook, Set Theory (Cambridge University Press, 1999, ISBN 052159667X). Some of his more well-cited research papers include
Other selected results include:
, and a second conference honoring the 70th birthdays of both Hajnal and Vera Sós was held in 2001 in Budapest
.
Rutgers University
Rutgers, The State University of New Jersey , is the largest institution for higher education in New Jersey, United States. It was originally chartered as Queen's College in 1766. It is the eighth-oldest college in the United States and one of the nine Colonial colleges founded before the American...
and a member of the Hungarian Academy of Sciences
Hungarian Academy of Sciences
The Hungarian Academy of Sciences is the most important and prestigious learned society of Hungary. Its seat is at the bank of the Danube in Budapest.-History:...
known for his work in set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
and combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
.
Biography
Hajnal was born on 13 May 1931, in HungaryHungary
Hungary , officially the Republic of Hungary , is a landlocked country in Central Europe. It is situated in the Carpathian Basin and is bordered by Slovakia to the north, Ukraine and Romania to the east, Serbia and Croatia to the south, Slovenia to the southwest and Austria to the west. The...
.
He received his university diploma (M.Sc. degree) in 1953 from the Eötvös Loránd University, his Candidate of Mathematical Science degree (roughly equivalent to Ph.D.) in 1957, under the supervision of László Kalmár
László Kalmár
László Kalmár was a Hungarian mathematician and Professor at the University of Szeged. Kalmár is considered the founder of mathematical logic and theoretical Computer Science in Hungary.- Biography :...
, and his Doctor of Mathematical Science degree in 1962. From 1956 to 1995 he was a faculty member at the Eötvös Loránd University; in 1994, he moved to Rutgers University to become the director of DIMACS
DIMACS
The Center for Discrete Mathematics and Theoretical Computer Science is a collaboration between Rutgers University, Princeton University, and the research firms AT&T, Bell Labs, Telcordia, and NEC. It was founded in 1989 with money from the National Science Foundation...
, and he remained there as a professor until his retirement in 2004. He became a member of the Hungarian Academy of Sciences in 1982, and directed its mathematical institute
Alfréd Rényi Institute of Mathematics
The Alfréd Rényi Institute of Mathematics is the research institute in mathematics of the Hungarian Academy of Sciences. It was created in 1950 by Alfréd Rényi, who directed it until his death. Since its creation, the institute has been the center of mathematical research in Hungary. It received...
from 1982 to 1992. He was general secretary of the János Bolyai Mathematical Society
János Bolyai Mathematical Society
The János Bolyai Mathematical Society is the Hungarian mathematical society, named after János Bolyai, a 19th century Hungarian mathematician, a co-discoverer of non-Euclidean geometry. It is the professional society of the Hungarian mathematicians, applied mathematicians, and mathematics teachers...
from 1980 to 1990, and president of the society from 1990 to 1994. Since 1981, he has been an advisory editor of the journal Combinatorica
Combinatorica
Combinatorica is an international journal of mathematics, publishing papers in the fields of combinatorics and computer science. It started in 1981, with László Babai and László Lovász as the editors-in-chief with Paul Erdős as honorary editor-in-chief. The current editors-in-chief are László...
.
In all his life, Hajnal has been an avid chess
Chess
Chess is a two-player board game played on a chessboard, a square-checkered board with 64 squares arranged in an eight-by-eight grid. It is one of the world's most popular games, played by millions of people worldwide at home, in clubs, online, by correspondence, and in tournaments.Each player...
player.
Hajnal is the father of Peter Hajnal, the co-dean of the European College of Liberal Arts
European College of Liberal Arts
The European College of Liberal Arts is a private, non-profit institution of higher education in Berlin, Germany. It was founded as a non-profit association in 1999 under the leadership of Stephan Gutzeit. The founding dean was Erika Anita Kiss. Since 2003, Peter Hajnal and Thomas Norgaard have...
.
Research and publications
Hajnal is the author of over 150 publications. Among the many co-authors of Paul ErdősPaul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
, he has the second largest number of joint papers, 56.
With Peter Hamburger, he wrote a textbook, Set Theory (Cambridge University Press, 1999, ISBN 052159667X). Some of his more well-cited research papers include
- A paper on circuit complexityCircuit complexityIn theoretical computer science, circuit complexity is a branch of computational complexity theory in which Boolean functions are classified according to the size or depth of Boolean circuits that compute them....
with Maas, Pudlak, SzegedyMario SzegedyMario Szegedy is a Hungarian computer scientist, professor of computer science at Rutgers University. He received his Ph.D. in computer science in 1989 from the University of Chicago...
, and György Turán, showing exponential lower bounds on the size of bounded-depth circuits with weighted majorityMajority functionIn Boolean logic, the majority function is a function from n inputs to one output. The value of the operation is false when n/2 or more arguments are false, and true otherwise....
gates that solve the problem of computing the parity of inner productsDot productIn mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
. - The Hajnal–Szemerédi theorem on equitable coloringEquitable coloringIn graph theory, an area of mathematics, an equitable coloring is an assignment of colors to the vertices of an undirected graph, in such a way that*No two adjacent vertices have the same color, and...
, proving a 1964 conjecture of Erdős: let Δ denote the maximum degree of a vertex in a finite graph G. Then G can be coloredGraph coloringIn graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the...
with Δ + 1 colors in such a way that the sizes of the color classes differ by at most one. Several authors have subsequently published simplifications and generalizations of this result. - A paper with Erdős and J. W. Moon on graphs that avoid having any k-cliqueClique (graph theory)In the mathematical area of graph theory, a clique in an undirected graph is a subset of its vertices such that every two vertices in the subset are connected by an edge. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs...
s. Turán's theoremTurán's theoremIn graph theory, Turán's theorem is a result on the number of edges in a Kr+1-free graph.An n-vertex graph that does not contain any -vertex clique may be formed by partitioning the set of vertices into r parts of equal or nearly-equal size, and connecting two vertices by an edge whenever they...
characterizes the graphs of this type with the maximum number of edges; Erdős, Hajnal and Moon find a similar characterization of the smallest maximalMaximal elementIn mathematics, especially in order theory, a maximal element of a subset S of some partially ordered set is an element of S that is not smaller than any other element in S. The term minimal element is defined dually...
k-clique-free graphs, showing that they take the form of certain split graphSplit graphIn graph theory, a branch of mathematics, a split graph is a graph in which the vertices can be partitioned into a clique and an independent set...
s. This paper also proves a conjecture of Erdős and GallaiTibor GallaiTibor Gallai was a Hungarian mathematician. He worked in combinatorics, especially in graph theory, and was a lifelong friend and collaborator of Paul Erdős. He was a student of Dénes König and an advisor of László Lovász...
on the number of edges in a critical graphCritical graphIn general the notion of criticality can refer to any measure.But in graph theory, when the term is used without any qualification, it almost always refers to the chromatic number of a graph....
for dominationDominating setIn graph theory, a dominating set for a graph G = is a subset D of V such that every vertex not in D is joined to at least one member of D by some edge...
. - A paper with Erdős on graph coloringGraph coloringIn graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the...
problems for infinite graphs and hypergraphHypergraphIn mathematics, a hypergraph is a generalization of a graph, where an edge can connect any number of vertices. Formally, a hypergraph H is a pair H = where X is a set of elements, called nodes or vertices, and E is a set of non-empty subsets of X called hyperedges or links...
s. This paper extends greedy coloringGreedy coloringIn the study of graph coloring problems in mathematics and computer science, a greedy coloring is a coloring of the vertices of a graph formed by a greedy algorithm that considers the vertices of the graph in sequence and assigns each vertex its first available color...
methods from finite to infinite graphs: if the vertices of a graph can be well-ordered so that each vertex has few earlier neighbors, it has low chromatic number. When every finite subgraph has an ordering of this type in which the number of previous neighbors is at most k (that is, it is k-degenerateDegeneracy (graph theory)In graph theory, a k-degenerate graph is an undirected graph in which every subgraph has a vertex of degree at most k: that is, some vertex in the subgraph touches k or fewer of the subgraph's edges. The degeneracy of a graph is the smallest value of k for which it is k-degenerate...
), an infinite graph has a well-ordering with at most 2k − 2 earlier neighbors per vertex. The paper also proves the nonexistence of infinite graphs with high finite girth and sufficiently large infinite chromatic number and the existence of graphs with high odd girth and infinite chromatic number.
Other selected results include:
- In his dissertation he introduced the models L(A) (see relative constructibility), and proved that if κ is a regular cardinalRegular cardinalIn set theory, a regular cardinal is a cardinal number that is equal to its own cofinality. So, crudely speaking, a regular cardinal is one which cannot be broken into a smaller collection of smaller parts....
and A is a subset of κ+, then ZFC and 2κ = κ+ hold in L(A). This can be applied to prove relative consistency results: e.g., if 2ℵ0 = ℵ2 is consistent then so is 2ℵ0 = ℵ2 and 2ℵ1 = ℵ2. - Hajnal's set mapping theorem, the solution to a conjecture of Stanisław Ruziewicz. This work concerns functions ƒ that map the members of an infinite set S to small subsets of S; more specifically, all subsets' cardinalities should be smaller than some upper bound that is itself smaller than the cardinality of S. Hajnal shows that S must have an equinumerous subset in which no pair of elements x and y have x in ƒ(y) and y in ƒ(x). This result greatly extends the case n = 1 of Kuratowski's free set theorem, which states that when ƒ maps an uncountable set to finite subsets there exists a pair x, y neither of which belongs to the image of the other.
- An example of two graphs each with uncountable chromatic number, but with countably chromatic direct product. That is, Hedetniemi's conjectureHedetniemi's conjectureIn graph theory, Hedetniemi's conjecture, named after Stephen T. Hedetniemi, concerns the connection between graph coloring and the tensor product of graphs...
fails for infinite graphs. - In a paper with Paul ErdősPaul ErdosPaul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
he proved several results on systems of infinite sets having property BProperty BIn mathematics, Property B is a certain set theoretic property. Formally, given a finite set X, a collection C of subsets of X, all of size n, has Property B if we can partition X into two disjoint subsets Y and Z such that every set in C meets both Y and Z...
. - A paper with Fred GalvinFred GalvinFrederick William Galvin is a mathematician, currently a professor at the University of Kansas. His research interests include set theory and combinatorics.His notable combinatorial work includes the proof of the Dinitz conjecture...
in which they proved that if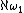
is a strong limit cardinalLimit cardinalIn mathematics, limit cardinals are certain cardinal numbers. A cardinal number λ is a weak limit cardinal if λ is neither a successor cardinal nor zero. This means that one cannot "reach" λ by repeated successor operations...
then
- This was the result which initiated ShelahSaharon ShelahSaharon Shelah is an Israeli mathematician. He is a professor of mathematics at the Hebrew University of Jerusalem and Rutgers University in New Jersey.-Biography:...
's pcf theoryPCF theoryPCF theory is the name of a mathematical theory, introduced by Saharon , that deals with the cofinality of the ultraproducts of ordered sets. It gives strong upper bounds on the cardinalities of power sets of singular cardinals, and has many more applications as well...
.- With James Earl BaumgartnerJames Earl BaumgartnerJames Earl Baumgartner is an American mathematician active in set theory, mathematical logic and foundations, and topology. He is an emeritus professor at Dartmouth College....
he proved a result in infinite Ramsey theoryRamsey theoryRamsey theory, named after the British mathematician and philosopher Frank P. Ramsey, is a branch of mathematics that studies the conditions under which order must appear...
, that for every partition of the vertices of a complete graphComplete graphIn the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
on ω1 vertices into finitely many subsets, at least one of the subsets contains a complete subgraph on α vertices, for every α < ω1. This can be expressed using the notation of partition relations as - With Matthew ForemanMatthew ForemanMatthew Dean Foreman is a set theorist at University of California, Irvine. He has made contributions in widely varying areas of set theory, including descriptive set theory, forcing, and infinitary combinatorics....
he proved that if κ is measurableMeasurable cardinal- Measurable :Formally, a measurable cardinal is an uncountable cardinal number κ such that there exists a κ-additive, non-trivial, 0-1-valued measure on the power set of κ...
then the partition relation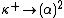
holds for α<Ω, where Ω<κ+ is a very large ordinal. - With István Juhász he published several results in set-theoretic topologySet-theoretic topologyIn mathematics, set-theoretic topology is a subject that combines set theory and general topology. It focuses on topological questions that are independent of ZFC. A famous problem is the normal Moore space question, a question in general topology that was the subject of intense research. The...
. They first established the existence of Hausdorff spaces which are hereditarily separable, but not hereditarily Lindelöf, or vice versa. The existence of regular spaces with these properties (S-space and L-space) was much later settled, by Todorcevic and Moore.
- With James Earl Baumgartner
Awards and honors
In 1992, Hajnal was awarded the Officer's Cross of the Order of the Republic of Hungary. In 1999, a conference in honor of his 70th birthday was held at DIMACSDIMACS
The Center for Discrete Mathematics and Theoretical Computer Science is a collaboration between Rutgers University, Princeton University, and the research firms AT&T, Bell Labs, Telcordia, and NEC. It was founded in 1989 with money from the National Science Foundation...
, and a second conference honoring the 70th birthdays of both Hajnal and Vera Sós was held in 2001 in Budapest
Budapest
Budapest is the capital of Hungary. As the largest city of Hungary, it is the country's principal political, cultural, commercial, industrial, and transportation centre. In 2011, Budapest had 1,733,685 inhabitants, down from its 1989 peak of 2,113,645 due to suburbanization. The Budapest Commuter...
.