
Property B
Encyclopedia
In mathematics
, Property B is a certain set theoretic
property. Formally, given a finite set X, a collection C of subset
s of X, all of size n, has Property B if we can partition X into two disjoint subsets Y and Z such that every set in C meets both Y and Z. The smallest number of sets in a collection of sets of size n such that C does not have Property B is denoted by m(n).
The property gets its name from mathematician Felix Bernstein
, who first introduced the property in 1908.
m(1)
m(2)
m(3)
m(4)
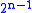 sets of size n, there exists a 2-coloring in which no set is monochromatic. The proof is simple: Consider a random coloring. The probability that any one set is monochromatic is
sets of size n, there exists a 2-coloring in which no set is monochromatic. The proof is simple: Consider a random coloring. The probability that any one set is monochromatic is 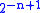 . By a union bound, the probability that any set is monochromatic is less than
. By a union bound, the probability that any set is monochromatic is less than 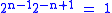 . Therefore, there exists a good coloring.
. Therefore, there exists a good coloring.
Erdős (1964) constructed an n-uniform graph with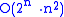 edges which does not have property B, establishing an upper bound. Schmidt (1963) proved that every collection of at most
edges which does not have property B, establishing an upper bound. Schmidt (1963) proved that every collection of at most 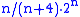 has property B. Erdős and Lovász conjectured that
has property B. Erdős and Lovász conjectured that 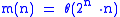 . Beck in 1978 improved the lower bound to
. Beck in 1978 improved the lower bound to  . In 2000, Radhakrishnan and Srinivasan improved the lower bound to
. In 2000, Radhakrishnan and Srinivasan improved the lower bound to 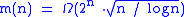 . They used a clever probabilistic algorithm.
. They used a clever probabilistic algorithm.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Property B is a certain set theoretic
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
property. Formally, given a finite set X, a collection C of subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of X, all of size n, has Property B if we can partition X into two disjoint subsets Y and Z such that every set in C meets both Y and Z. The smallest number of sets in a collection of sets of size n such that C does not have Property B is denoted by m(n).
The property gets its name from mathematician Felix Bernstein
Felix Bernstein
Felix Bernstein was a German Jewish mathematician known for developing a theorem of the equivalence of sets in 1897, and less well known for demonstrating the correct blood group inheritance pattern of multiple alleles at one locus in 1924 through statistical analysis...
, who first introduced the property in 1908.
Values of m(n)
It is known that m(1) = 1, m(2) = 3, and m(3) = 7 (as can by seen by the following examples); the value of m(4) is not known, although an upper bound of 23 (Seymour, Toft) and a lower bound of 21 (Manning) have been proven. At the time of this writing (August 2004), there is no OEIS entry for the sequence m(n) yet, due to the lack of terms known.m(1)
- For n = 1, set X = {1}, and C =
. Then C does not have Property B.
m(2)
- For n = 2, set X = {1, 2, 3} and C = . Then C does not have Property B, so m(2) <= 3. However, C
' = does (set Y = {1} and Z = {2, 3}), so m(2) >= 3.
m(3)
- For n = 3, set X = {1, 2, 3, 4, 5, 6, 7}, and C = (the Steiner triple system S7); C does not have Property B (so m(3) <= 7), but if any element of C is omitted, then that element can be taken as Y, and the set of remaining elements C
' will have Property B (so for this particular case, m(3) >= 7). One may check all other collections of 6 3-sets to see that all have Property B.
m(4)
- Seymour (1974) constructed a hypergraph on 11 vertices with 23 edges withouth Property B, which shows that m(4) <= 23. Manning (1995) proved that m(4) >= 20.
Asymptotics of m(n)
Erdős (1963) proved that for any collection of fewer than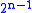 sets of size n, there exists a 2-coloring in which no set is monochromatic. The proof is simple: Consider a random coloring. The probability that any one set is monochromatic is
sets of size n, there exists a 2-coloring in which no set is monochromatic. The proof is simple: Consider a random coloring. The probability that any one set is monochromatic is 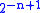 . By a union bound, the probability that any set is monochromatic is less than
. By a union bound, the probability that any set is monochromatic is less than 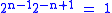 . Therefore, there exists a good coloring.
. Therefore, there exists a good coloring.Erdős (1964) constructed an n-uniform graph with
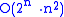 edges which does not have property B, establishing an upper bound. Schmidt (1963) proved that every collection of at most
edges which does not have property B, establishing an upper bound. Schmidt (1963) proved that every collection of at most 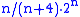 has property B. Erdős and Lovász conjectured that
has property B. Erdős and Lovász conjectured that 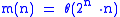 . Beck in 1978 improved the lower bound to
. Beck in 1978 improved the lower bound to  . In 2000, Radhakrishnan and Srinivasan improved the lower bound to
. In 2000, Radhakrishnan and Srinivasan improved the lower bound to 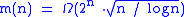 . They used a clever probabilistic algorithm.
. They used a clever probabilistic algorithm.

