
Ambient construction
Encyclopedia
In conformal geometry
, the ambient construction refers to a construction of Charles Fefferman
and Robin Graham for which a conformal manifold of dimension n is realized (ambiently) as the boundary of a certain Poincaré manifold
, or alternatively as the celestial sphere
of a certain pseudo-Riemannian manifold.
The ambient construction is canonical in the sense that it is performed only using the conformal class of the metric: it is conformally invariant. However, the construction only works asymptotically, up to a certain order of approximation. There is, in general, an obstruction to continuing this extension past the critical order. The obstruction itself is of tensorial character, and is known as the (conformal) obstruction tensor. It is, along with the Weyl tensor
, one of the two primitive invariants in conformal differential geometry.
Aside from the obstruction tensor, the ambient construction can be used to define a class of conformally invariant differential operator
s known as the GJMS operator
s.
A related construction is the tractor bundle
.
, with the origin deleted. The celestial sphere at infinity is the conformal manifold M, and the null rays in the cone determine a line bundle
over M. Moreover, the null cone carries a metric which degenerates in the direction of the generators of the cone.
The ambient construction in this flat model space then asks: if one is provided with such a line bundle, along with its degenerate metric, to what extent is it possible to extend the metric off the null cone in a canonical way, thus recovering the ambient Minkowski space? In formal terms, the degenerate metric supplies a Dirichlet boundary condition
for the extension problem and, as it happens, the natural condition is for the extended metric to be Ricci flat (because of the normalization of the normal conformal connection.)
The ambient construction generalizes this to the case when M is conformally curved, first by constructing a natural null line bundle N with a degenerate metric, and then solving the associated Dirichlet problem on N × (-1,1).

Moreover, the total space of N carries a tautological degenerate metric, for if p is a point of the fibre of π : N → M corresponding to the conformal representative gp, then let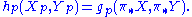
This metric degenerates along the vertical directions. Furthermore, it is homogeneous of degree 2 under the R+ action on N:
Let X be the vertical vector field generating the scaling action. Then the following properties are immediate:
An ambient metric on N~ is a Lorentzian metric h~ such that
Suppose that a fixed representative of the conformal metric g and a local coordinate system x = (xi) are chosen on M. These induce coordinates on N by identifying a point in the fibre of N with (x,t2g(x)) where t > 0 is the fibre coordinate. (In these coordinates, X = t ∂t.) Finally, if ρ is a defining function of N in N~ which is homogeneous of degree 0 under dilations, then (x,t,ρ) are coordinates of N~. Furthermore, any extension metric which is homogeneous of degree 2 can be written in these coordinates in the form: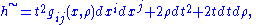
where the gij are n2 functions with g(x,0) = g(x), the given conformal representative.
After some calculation one shows that the Ricci flatness is equivalent to the following differential equation, where the prime is differentiation with respect to ρ: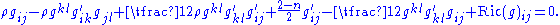
One may then formally solve this equation as a power series in ρ to obtain the asymptotic development of the ambient metric off the null cone. For example, substituting ρ = 0 and solving gives
where P is the Schouten tensor. Next, differentiating again and substituting the known value of gij′(x,0) into the equation, the second derivative can be found to be a multiple of the Bach tensor
. And so forth.
Conformal geometry
In mathematics, conformal geometry is the study of the set of angle-preserving transformations on a space. In two real dimensions, conformal geometry is precisely the geometry of Riemann surfaces...
, the ambient construction refers to a construction of Charles Fefferman
Charles Fefferman
Charles Louis Fefferman is an American mathematician at Princeton University. His primary field of research is mathematical analysis....
and Robin Graham for which a conformal manifold of dimension n is realized (ambiently) as the boundary of a certain Poincaré manifold
Hyperbolic manifold
In mathematics, a hyperbolic n-manifold is a complete Riemannian n-manifold of constant sectional curvature -1.Every complete, connected, simply-connected manifold of constant negative curvature −1 is isometric to the real hyperbolic space Hn. As a result, the universal cover of any closed manifold...
, or alternatively as the celestial sphere
Celestial sphere
In astronomy and navigation, the celestial sphere is an imaginary sphere of arbitrarily large radius, concentric with the Earth and rotating upon the same axis. All objects in the sky can be thought of as projected upon the celestial sphere. Projected upward from Earth's equator and poles are the...
of a certain pseudo-Riemannian manifold.
The ambient construction is canonical in the sense that it is performed only using the conformal class of the metric: it is conformally invariant. However, the construction only works asymptotically, up to a certain order of approximation. There is, in general, an obstruction to continuing this extension past the critical order. The obstruction itself is of tensorial character, and is known as the (conformal) obstruction tensor. It is, along with the Weyl tensor
Weyl tensor
In differential geometry, the Weyl curvature tensor, named after Hermann Weyl, is a measure of the curvature of spacetime or, more generally, a pseudo-Riemannian manifold. Like the Riemann curvature tensor, the Weyl tensor expresses the tidal force that a body feels when moving along a geodesic...
, one of the two primitive invariants in conformal differential geometry.
Aside from the obstruction tensor, the ambient construction can be used to define a class of conformally invariant differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
s known as the GJMS operator
GJMS operator
In the mathematical field of differential geometry, the GJMS operators are a family of differential operators, that are defined on a Riemannian manifold. In an appropriate sense, they depend only on the conformal structure of the manifold. The GJMS operators generalize the Paneitz operator and...
s.
A related construction is the tractor bundle
Tractor bundle
In conformal geometry, the tractor bundle is a particular vector bundle constructed on a conformal manifold whose fibres form an effective representation of the conformal group ....
.
Overview
The model flat geometry for the ambient construction is the future null cone in Minkowski spaceMinkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
, with the origin deleted. The celestial sphere at infinity is the conformal manifold M, and the null rays in the cone determine a line bundle
Line bundle
In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
over M. Moreover, the null cone carries a metric which degenerates in the direction of the generators of the cone.
The ambient construction in this flat model space then asks: if one is provided with such a line bundle, along with its degenerate metric, to what extent is it possible to extend the metric off the null cone in a canonical way, thus recovering the ambient Minkowski space? In formal terms, the degenerate metric supplies a Dirichlet boundary condition
Dirichlet boundary condition
In mathematics, the Dirichlet boundary condition is a type of boundary condition, named after Johann Peter Gustav Lejeune Dirichlet who studied under Cauchy and succeeded Gauss at University of Göttingen. When imposed on an ordinary or a partial differential equation, it specifies the values a...
for the extension problem and, as it happens, the natural condition is for the extended metric to be Ricci flat (because of the normalization of the normal conformal connection.)
The ambient construction generalizes this to the case when M is conformally curved, first by constructing a natural null line bundle N with a degenerate metric, and then solving the associated Dirichlet problem on N × (-1,1).
Details
This section provides an overview of the construction, first of the null line bundle, and then of its ambient extension.The null line bundle
Suppose that M is a conformal manifold, and that [g] denotes the conformal metric defined on M. Let π : N → M denote the tautological subbundle of T*M ⊗ T*M defined by all representatives of the conformal metric. In terms of a fixed background metric g0, N consists of all positive multiples ω2g0 of the metric. There is a natural action of R+ on N, given by
Moreover, the total space of N carries a tautological degenerate metric, for if p is a point of the fibre of π : N → M corresponding to the conformal representative gp, then let
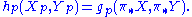
This metric degenerates along the vertical directions. Furthermore, it is homogeneous of degree 2 under the R+ action on N:

Let X be the vertical vector field generating the scaling action. Then the following properties are immediate:
- h(X,-) = 0
- LXh = 2h, where LX is the Lie derivativeLie derivativeIn mathematics, the Lie derivative , named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a vector field or more generally a tensor field, along the flow of another vector field...
along the vector field X.
The ambient space
Let N~ = N × (-1,1), with the natural inclusion i : N → N~. The dilations δω extend naturally to N~, and hence so does the generator X of dilation.An ambient metric on N~ is a Lorentzian metric h~ such that
- The metric is homogeneous: δω* h~ = ω2 h~
- The metric is an ambient extension: i* h~ = h, where i* is the pullback along the natural inclusion.
- The metric is Ricci flat: Ric(h~) = 0.
Suppose that a fixed representative of the conformal metric g and a local coordinate system x = (xi) are chosen on M. These induce coordinates on N by identifying a point in the fibre of N with (x,t2g(x)) where t > 0 is the fibre coordinate. (In these coordinates, X = t ∂t.) Finally, if ρ is a defining function of N in N~ which is homogeneous of degree 0 under dilations, then (x,t,ρ) are coordinates of N~. Furthermore, any extension metric which is homogeneous of degree 2 can be written in these coordinates in the form:
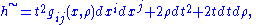
where the gij are n2 functions with g(x,0) = g(x), the given conformal representative.
After some calculation one shows that the Ricci flatness is equivalent to the following differential equation, where the prime is differentiation with respect to ρ:
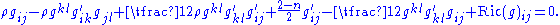
One may then formally solve this equation as a power series in ρ to obtain the asymptotic development of the ambient metric off the null cone. For example, substituting ρ = 0 and solving gives
- gij′(x,0) = 2Pij
where P is the Schouten tensor. Next, differentiating again and substituting the known value of gij′(x,0) into the equation, the second derivative can be found to be a multiple of the Bach tensor
Bach tensor
In differential geometry and general relativity, the Bach tensor is a tensor of rank 2 which is conformally invariant in dimension n=4. It is the only known conformally invariant tensor that is algebraically independent of the Weyl tensor...
. And so forth.

