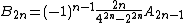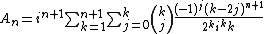Alternating permutation
Encyclopedia
In combinatorial
mathematics
, an alternating permutation of the set {1, 2, 3, ..., n} is an arrangement of those numbers into an order c1, ..., cn such that no element ci is between ci − 1 and ci + 1 for any value of i and c1< c2. In other words, ci < ci+ 1 if i is odd and ci > ci+ 1 if i is even. For example, the five alternating permutations of {1, 2, 3, 4} are:
This type of permutation was first studied by Désiré André in the 19th century.
If the condition c1< c2 is dropped, so we only require that no element ci is between ci − 1 and ci + 1, then the permutation is called a zigzag permutation. By exchanging 1 with n, 2 with n − 1, etc., each zigzag permutation with c1> c2 can be paired uniquely with an alternating permutation.
The numbers A2n with even indices are called secant numbers or zig numbers. The first few values are 1, 1, 5, 61, 1385, 50521, ... . They appear as numerators in the Maclaurin series of sec x. Specifically,
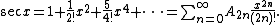
Secant numbers are related to Euler numbers by the formula E2n = (−1)nA2n. (En = 0 when n is odd.)
Correspondingly, the numbers A2n+1 with odd indices are called tangent numbers or zag numbers. The first few values are 1, 2, 16, 272, 7936, ... . They appear as numerators in the Maclaurin series of tan x. Specifically,
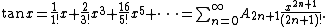
Tangent numbers are related to Bernoulli numbers by the formula
for n > 0.
Adding these series together gives the exponential generating function of the sequence
An:
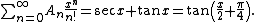
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an alternating permutation of the set {1, 2, 3, ..., n} is an arrangement of those numbers into an order c1, ..., cn such that no element ci is between ci − 1 and ci + 1 for any value of i and c1< c2. In other words, ci < ci+ 1 if i is odd and ci > ci+ 1 if i is even. For example, the five alternating permutations of {1, 2, 3, 4} are:
- 1, 3, 2, 4 because 1 < 3 > 2 < 4
- 1, 4, 2, 3 because 1 < 4 > 2 < 3
- 2, 3, 1, 4 because 2 < 3 > 1 < 4
- 2, 4, 1, 3 because 2 < 4 > 1 < 3
- 3, 4, 1, 2 because 3 < 4 > 1 < 2
This type of permutation was first studied by Désiré André in the 19th century.
If the condition c1< c2 is dropped, so we only require that no element ci is between ci − 1 and ci + 1, then the permutation is called a zigzag permutation. By exchanging 1 with n, 2 with n − 1, etc., each zigzag permutation with c1> c2 can be paired uniquely with an alternating permutation.
Related integer sequences
The determination of the number, An, of alternating permutations of the set {1, ..., n} is called André's problem. If Zn denotes the number of zigzag permutations of {1, ..., n} then it is clear from the pairing given above that Zn = 2An for n ≥ 2. The numbers An are known as Euler zigzag numbers or Up/down numbers. The first few values of An are 1, 1, 1, 2, 5, 16, 61, 272, 1385, 7936, 50521, ... . The first few values of Zn are 1, 1, 2, 4, 10, 32, 122, 544, 2770, 15872, 101042, ... .The numbers A2n with even indices are called secant numbers or zig numbers. The first few values are 1, 1, 5, 61, 1385, 50521, ... . They appear as numerators in the Maclaurin series of sec x. Specifically,
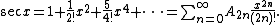
Secant numbers are related to Euler numbers by the formula E2n = (−1)nA2n. (En = 0 when n is odd.)
Correspondingly, the numbers A2n+1 with odd indices are called tangent numbers or zag numbers. The first few values are 1, 2, 16, 272, 7936, ... . They appear as numerators in the Maclaurin series of tan x. Specifically,
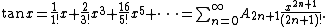
Tangent numbers are related to Bernoulli numbers by the formula
for n > 0.
Adding these series together gives the exponential generating function of the sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
An:
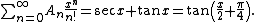
See also
- Boustrophedon transformBoustrophedon transformIn mathematics, the boustrophedon transform is a procedure which maps one sequence to another. The transformed sequence is computed by filling a triangular array in boustrophedon manner.-Definition:...
- Fence (mathematics)Fence (mathematics)In mathematics, a fence, also called a zigzag poset, is a partially ordered set in which the order relations form a path with alternating orientations:orA fence may be finite, or it may be formed by an infinite alternating sequence extending in both directions.A linear extension of a fence is...
, partially ordered sets that have alternating permutations as their linear extensions
External links
- Ross Tang, "An Explicit Formula for the Euler zigzag numbers (Up/down numbers) from power series" A simple explicit formula for An.