Boustrophedon transform
Encyclopedia
In mathematics
, the boustrophedon transform is a procedure which maps one sequence to another. The transformed sequence is computed by filling a triangular array
in boustrophedon
(zig-zag) manner.
Given a sequence 
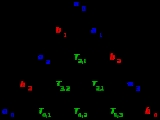
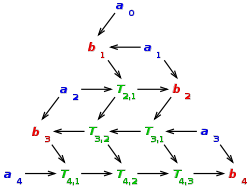
, the boustrophedon transform yields another sequence,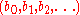 
, which is constructed by filling up a triangle as pictured on the right. Number the rows in the triangle starting from 0, and fill the rows consecutively. Let k denote the number of the row currently being filled.
If k is odd, then put the number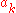
on the right end of the row and fill the row from the right to the left, with every entry being the sum of the number to the right and the number to the upper right. If k is even, then put the number 
on the left end and fill the row from the left to the right, with every entry being the sum of the number to the left and the number to the upper left.
The numbers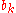
forming the transformed sequence can then be found on the left end of odd-numbered rows and on the right end of even-numbered rows, that is, opposite to the numbers 
.
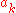. Define the numbers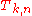
(with k ≥ n ≥ 0) by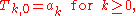
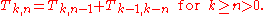
Then the transformed sequence is defined by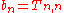
.
In the case a0 = 1, an = 0 (n > 0), the resulting triangle is called the Seidel–Entringer–Arnold Triangle and the numbers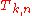
are called Entringer numbers . In this case the numbers in the transformed sequence bn are called the Euler up/down numbers. This is sequence A000111 on the On-Line Encyclopedia of Integer Sequences
. These enumerate the number of alternating permutations on n letters and are related to the Euler numbers and the Bernoulli number
s.
The exponential generating function of the boustrophedon transform (bn) is related to that of the original sequence (an) by
The exponential generating function of the unit sequence is 1, so that of the up/down numbers is sec x + tan x.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the boustrophedon transform is a procedure which maps one sequence to another. The transformed sequence is computed by filling a triangular array
Triangular array
In mathematics and computing, a triangular array of numbers, polynomials, or the like, is a doubly indexed sequence in which each row is only as long as the row's own index.Notable particular examples include these:...
in boustrophedon
Boustrophedon
Boustrophedon , is a type of bi-directional text, mostly seen in ancient manuscripts and other inscriptions. Every other line of writing is flipped or reversed, with reversed letters. Rather than going left-to-right as in modern English, or right-to-left as in Arabic and Hebrew, alternate lines in...
(zig-zag) manner.
Definition
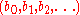, the boustrophedon transform yields another sequence, , which is constructed by filling up a triangle as pictured on the right. Number the rows in the triangle starting from 0, and fill the rows consecutively. Let k denote the number of the row currently being filled.If k is odd, then put the number
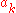on the right end of the row and fill the row from the right to the left, with every entry being the sum of the number to the right and the number to the upper right. If k is even, then put the number on the left end and fill the row from the left to the right, with every entry being the sum of the number to the left and the number to the upper left.The numbers
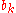forming the transformed sequence can then be found on the left end of odd-numbered rows and on the right end of even-numbered rows, that is, opposite to the numbers 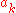.Recurrence relation
A more formal definition uses a recurrence relationRecurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
. Define the numbers
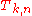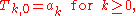
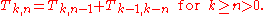
(with k ≥ n ≥ 0) byThen the transformed sequence is defined by
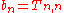.In the case a0 = 1, an = 0 (n > 0), the resulting triangle is called the Seidel–Entringer–Arnold Triangle and the numbers
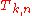are called Entringer numbers . In this case the numbers in the transformed sequence bn are called the Euler up/down numbers. This is sequence A000111 on the On-Line Encyclopedia of Integer SequencesOn-Line Encyclopedia of Integer Sequences
The On-Line Encyclopedia of Integer Sequences , also cited simply as Sloane's, is an online database of integer sequences, created and maintained by N. J. A. Sloane, a researcher at AT&T Labs...
. These enumerate the number of alternating permutations on n letters and are related to the Euler numbers and the Bernoulli number
Bernoulli number
In mathematics, the Bernoulli numbers Bn are a sequence of rational numbers with deep connections to number theory. They are closely related to the values of the Riemann zeta function at negative integers....
s.
The exponential generating function
The exponential generating function of a sequence (an) is defined byThe exponential generating function of the boustrophedon transform (bn) is related to that of the original sequence (an) by
The exponential generating function of the unit sequence is 1, so that of the up/down numbers is sec x + tan x.