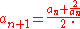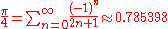Aitken's delta-squared process
Encyclopedia
In numerical analysis
, Aitken's delta-squared process is a series acceleration
method, used for accelerating the rate of convergence
of a sequence. It is named after Alexander Aitken
, who introduced this method in 1926. Its early form was known to Seki Kōwa (end of 17th century) and was found for rectification of the circle, i.e. the calculation of π. It is most useful for accelerating the convergence of a sequence that is converging linearly.
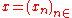 , one associates to this sequence the new sequence
, one associates to this sequence the new sequence
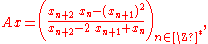
which can also be written as
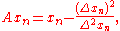
where
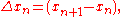
and
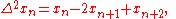
for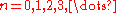
(To use this nice operator notation, one has to allow for the indices to start from n = 2 on, or apply a translation operator which first shifts the sequence indices by two, or to adopt the convention that xn = 0 for all n < 0.)
Obviously, Ax is ill-defined if Δ2x contains a zero element, or equivalently, if the sequence of first differences has a repeating term. From a theoretical point of view, assuming that this occurs only for a finite number of indices, one could easily agree to consider the sequence Ax restricted to indices n>n0 with a sufficiently large n0. From a practical point of view, one does in general rather consider only the first few terms of the sequence, which usually provide the needed precision. Moreover, when numerically computing the sequence, one has to take care to stop the computation when rounding errors become too important in the denominator, where the Δ² operation may cancel too many significant digits.
 will converge linearly
will converge linearly
to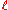 if there exists a number μ ∈ (0, 1) such that
if there exists a number μ ∈ (0, 1) such that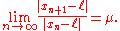
Aitken's method will accelerate the sequence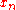 if
if 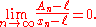
 is not a linear operator, but a constant term drops out, viz:
is not a linear operator, but a constant term drops out, viz:  , if
, if 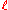 is a constant. This is clear from the expression of
is a constant. This is clear from the expression of 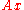 in terms of the finite difference
in terms of the finite difference
operator .
.
Although the new process does not in general converge quadratically, it can be shown that for a fixed point
process, that is, for an iterated function
sequence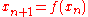 for some function
for some function  , converging to a fixed point, the convergence is quadratic. In this case, the technique is known as Steffensen's method
, converging to a fixed point, the convergence is quadratic. In this case, the technique is known as Steffensen's method
.
Empirically, the A-operation eliminates the "most important error term". One can check this by considering a sequence of the form , where
, where  :
:
The sequence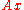 will then go to the limit like
will then go to the limit like 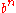 goes to zero.
goes to zero.
One can also show that if goes to its limit
goes to its limit 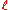 at a rate strictly greater than 1,
at a rate strictly greater than 1, 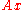 does not have a better rate of convergence. (In practice, one rarely has e.g. quadratic convergence which would mean over 30 resp. 100 correct decimal places after 5 resp. 7 iterations (starting with 1 correct digit); usually no acceleration is needed in that case.)
does not have a better rate of convergence. (In practice, one rarely has e.g. quadratic convergence which would mean over 30 resp. 100 correct decimal places after 5 resp. 7 iterations (starting with 1 correct digit); usually no acceleration is needed in that case.)
In practice,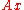 converges much faster to the limit than
converges much faster to the limit than  does, as demonstrated by the example calculations below.
does, as demonstrated by the example calculations below.
Usually, it is much cheaper to calculate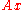 (involving only calculation of differences, one multiplication and one division) than to calculate many more terms of the sequence
(involving only calculation of differences, one multiplication and one division) than to calculate many more terms of the sequence  . Care must be taken, however, to avoid introducing errors due to insufficient precision when calculating the differences in the numerator and denominator of the expression.
. Care must be taken, however, to avoid introducing errors due to insufficient precision when calculating the differences in the numerator and denominator of the expression.
Starting with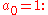
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, Aitken's delta-squared process is a series acceleration
Series acceleration
In mathematics, series acceleration is one of a collection of sequence transformations for improving the rate of convergence of a series. Techniques for series acceleration are often applied in numerical analysis, where they are used to improve the speed of numerical integration...
method, used for accelerating the rate of convergence
Rate of convergence
In numerical analysis, the speed at which a convergent sequence approaches its limit is called the rate of convergence. Although strictly speaking, a limit does not give information about any finite first part of the sequence, this concept is of practical importance if we deal with a sequence of...
of a sequence. It is named after Alexander Aitken
Alexander Aitken
Alexander Craig Aitken was one of New Zealand's greatest mathematicians. He studied for a PhD at the University of Edinburgh, where his dissertation, "Smoothing of Data", was considered so impressive that he was awarded a DSc in 1926, and was elected a fellow of the Royal Society of Edinburgh...
, who introduced this method in 1926. Its early form was known to Seki Kōwa (end of 17th century) and was found for rectification of the circle, i.e. the calculation of π. It is most useful for accelerating the convergence of a sequence that is converging linearly.
Definition
Given a sequence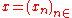 , one associates to this sequence the new sequence
, one associates to this sequence the new sequence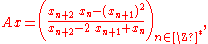
which can also be written as
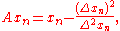
where
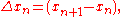
and
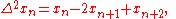
for
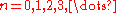
(To use this nice operator notation, one has to allow for the indices to start from n = 2 on, or apply a translation operator which first shifts the sequence indices by two, or to adopt the convention that xn = 0 for all n < 0.)
Obviously, Ax is ill-defined if Δ2x contains a zero element, or equivalently, if the sequence of first differences has a repeating term. From a theoretical point of view, assuming that this occurs only for a finite number of indices, one could easily agree to consider the sequence Ax restricted to indices n>n0 with a sufficiently large n0. From a practical point of view, one does in general rather consider only the first few terms of the sequence, which usually provide the needed precision. Moreover, when numerically computing the sequence, one has to take care to stop the computation when rounding errors become too important in the denominator, where the Δ² operation may cancel too many significant digits.
Properties
Aitken's delta-squared process is a method of acceleration of convergence, and a particular case of a nonlinear sequence transformation. will converge linearly
will converge linearlyRate of convergence
In numerical analysis, the speed at which a convergent sequence approaches its limit is called the rate of convergence. Although strictly speaking, a limit does not give information about any finite first part of the sequence, this concept is of practical importance if we deal with a sequence of...
to
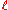 if there exists a number μ ∈ (0, 1) such that
if there exists a number μ ∈ (0, 1) such that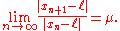
Aitken's method will accelerate the sequence
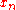 if
if 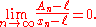
 is not a linear operator, but a constant term drops out, viz:
is not a linear operator, but a constant term drops out, viz:  , if
, if 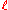 is a constant. This is clear from the expression of
is a constant. This is clear from the expression of 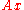 in terms of the finite difference
in terms of the finite differenceFinite difference
A finite difference is a mathematical expression of the form f − f. If a finite difference is divided by b − a, one gets a difference quotient...
operator
 .
.Although the new process does not in general converge quadratically, it can be shown that for a fixed point
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
process, that is, for an iterated function
Iterated function
In mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
sequence
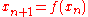 for some function
for some function  , converging to a fixed point, the convergence is quadratic. In this case, the technique is known as Steffensen's method
, converging to a fixed point, the convergence is quadratic. In this case, the technique is known as Steffensen's methodSteffensen's method
In numerical analysis, Steffensen's method is a root-finding method, similar to Newton's method, named after Johan Frederik Steffensen. Steffensen's method also achieves quadratic convergence, but without using derivatives as Newton's method does....
.
Empirically, the A-operation eliminates the "most important error term". One can check this by considering a sequence of the form
 , where
, where  :
:The sequence
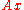 will then go to the limit like
will then go to the limit like 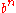 goes to zero.
goes to zero.One can also show that if
 goes to its limit
goes to its limit 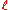 at a rate strictly greater than 1,
at a rate strictly greater than 1, 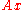 does not have a better rate of convergence. (In practice, one rarely has e.g. quadratic convergence which would mean over 30 resp. 100 correct decimal places after 5 resp. 7 iterations (starting with 1 correct digit); usually no acceleration is needed in that case.)
does not have a better rate of convergence. (In practice, one rarely has e.g. quadratic convergence which would mean over 30 resp. 100 correct decimal places after 5 resp. 7 iterations (starting with 1 correct digit); usually no acceleration is needed in that case.)In practice,
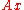 converges much faster to the limit than
converges much faster to the limit than  does, as demonstrated by the example calculations below.
does, as demonstrated by the example calculations below.Usually, it is much cheaper to calculate
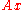 (involving only calculation of differences, one multiplication and one division) than to calculate many more terms of the sequence
(involving only calculation of differences, one multiplication and one division) than to calculate many more terms of the sequence  . Care must be taken, however, to avoid introducing errors due to insufficient precision when calculating the differences in the numerator and denominator of the expression.
. Care must be taken, however, to avoid introducing errors due to insufficient precision when calculating the differences in the numerator and denominator of the expression.Example calculations
- The value of
 may be approximated by assuming an initial value for
may be approximated by assuming an initial value for 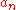 and iterating the following:
and iterating the following:
Starting with
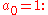
| n | x = iterated value | Ax |
| 0 | 1 | 1.4285714 |
| 1 | 1.5 | 1.4141414 |
| 2 | 1.4166667 | 1.4142136 |
| 3 | 1.4142157 | -- |
| 4 | 1.4142136 | -- |
- The value of
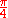 may be calculated as an infinite sum:
may be calculated as an infinite sum:
| n | term | x = partial sum | Ax |
| 0 | 1 | 1 | 0.79166667 |
| 1 | −0.33333333 | 0.66666667 | 0.78333333 |
| 2 | 0.2 | 0.86666667 | 0.78630952 |
| 3 | −0.14285714 | 0.72380952 | 0.78492063 |
| 4 | 0.11111111 | 0.83492063 | 0.78567821 |
| 5 | −9.0909091×10−2 | 0.74401154 | 0.78522034 |
| 6 | 7.6923077×10−2 | 0.82093462 | 0.78551795 |
| 7 | -6.6666667×10−2 | 0.75426795 | -- |
| 8 | 5.8823529×10−2 | 0.81309148 | -- |
See also
- Rate of convergenceRate of convergenceIn numerical analysis, the speed at which a convergent sequence approaches its limit is called the rate of convergence. Although strictly speaking, a limit does not give information about any finite first part of the sequence, this concept is of practical importance if we deal with a sequence of...
- Limit of a sequenceLimit of a sequenceThe limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
- Fixed point iteration
- Sequence transformation
- Shanks transformationShanks transformationIn numerical analysis, the Shanks transformation is a non-linear series acceleration method to increase the rate of convergence of a sequence. This method is named after Daniel Shanks, who rediscovered this sequence transformation in 1955. It was first derived and published by R...
- Steffensen's methodSteffensen's methodIn numerical analysis, Steffensen's method is a root-finding method, similar to Newton's method, named after Johan Frederik Steffensen. Steffensen's method also achieves quadratic convergence, but without using derivatives as Newton's method does....