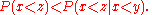Fishburn–Shepp inequality
Encyclopedia
In combinatorial
mathematics, the Fishburn–Shepp inequality is an inequality for the number of extensions of partial orders to linear orders, found by and .
It states that if x, y, and z are incomparable elements of a finite poset, then
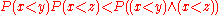
where P(*) is the probability that a linear order < extending the partial order has the property *.
In other words the probability that x < z strictly increases if one adds the condition that x < y. In the language of conditional probability
,
The proof uses the Ahlswede–Daykin inequality
.
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
mathematics, the Fishburn–Shepp inequality is an inequality for the number of extensions of partial orders to linear orders, found by and .
It states that if x, y, and z are incomparable elements of a finite poset, then
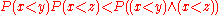
where P(*) is the probability that a linear order < extending the partial order has the property *.
In other words the probability that x < z strictly increases if one adds the condition that x < y. In the language of conditional probability
Conditional probability
In probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B...
,
The proof uses the Ahlswede–Daykin inequality
Ahlswede–Daykin inequality
A fundamental tool in statistical mechanics and probabilistic combinatorics , the Ahlswede–Daykin inequality is a correlation-type inequality for four functions on a finite distributive lattice....
.