
Adequate equivalence relation
Encyclopedia
In algebraic geometry
, a branch of mathematics
, an adequate equivalence relation is an equivalence relation on algebraic cycles of smooth projective varieties used to obtain a well-working theory of such cycles, and in particular, well-defined intersection products
. Samuel formalized the concept of an adequate equivalence relation in 1958. Since then it has become central to theory of motives. For every adequate equivalence relation, one may define the category of pure motives
with respect to that relation.
Possible (and useful) adequate equivalence relations include rational, algebraic, homological and numerical equivalence. They are called "adequate" because dividing out by the equivalence relation is functorial, i.e. push-forward (with change of co-dimension) and pull-back of cycles is well-defined. Codimension one cycles modulo rational equivalence form the classical group of divisor
s. All cycles modulo rational equivalence form the Chow ring
.
s, ∼X on Z*(X), one for each smooth projective variety X, satisfying the following three conditions:
The push-forward cycle in the last axiom is often denoted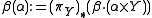
If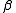 is the graph of a function, then this reduces to the push-forward of the function. The generalizations of functions from X to Y to cycles on X × Y are known as correspondences
is the graph of a function, then this reduces to the push-forward of the function. The generalizations of functions from X to Y to cycles on X × Y are known as correspondences
. The last axiom allows us to push forward cycles by a correspondence.
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an adequate equivalence relation is an equivalence relation on algebraic cycles of smooth projective varieties used to obtain a well-working theory of such cycles, and in particular, well-defined intersection products
Intersection theory
In mathematics, intersection theory is a branch of algebraic geometry, where subvarieties are intersected on an algebraic variety, and of algebraic topology, where intersections are computed within the cohomology ring. The theory for varieties is older, with roots in Bézout's theorem on curves and...
. Samuel formalized the concept of an adequate equivalence relation in 1958. Since then it has become central to theory of motives. For every adequate equivalence relation, one may define the category of pure motives
Motive (algebraic geometry)
In algebraic geometry, a motive denotes 'some essential part of an algebraic variety'. To date, pure motives have been defined, while conjectural mixed motives have not. Pure motives are triples , where X is a smooth projective variety, p : X ⊢ X is an idempotent correspondence, and m an integer...
with respect to that relation.
Possible (and useful) adequate equivalence relations include rational, algebraic, homological and numerical equivalence. They are called "adequate" because dividing out by the equivalence relation is functorial, i.e. push-forward (with change of co-dimension) and pull-back of cycles is well-defined. Codimension one cycles modulo rational equivalence form the classical group of divisor
Divisor (algebraic geometry)
In algebraic geometry, divisors are a generalization of codimension one subvarieties of algebraic varieties; two different generalizations are in common use, Cartier divisors and Weil divisors...
s. All cycles modulo rational equivalence form the Chow ring
Chow ring
In algebraic geometry, the Chow ring of an algebraic variety is an algebraic-geometric analogue of the cohomology ring of the variety considered as a topological space: its elements are formed out of actual subvarieties and its multiplicative structure is derived from the intersection of...
.
Definition
Let Z*(X) := Z[X] be the free abelian group on the algebraic cycles of X. Then an adequate equivalence relation is a family of equivalence relationEquivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
s, ∼X on Z*(X), one for each smooth projective variety X, satisfying the following three conditions:
- (Linearity) The equivalence relation is compatible with addition of cycles.
- (Moving lemma) If
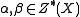 are cycles on X, then there exists a cycle
are cycles on X, then there exists a cycle 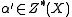 such that
such that  ~X
~X  and
and  intersects
intersects 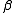 properly.
properly. - (Push-forwards) Let
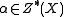 and
and 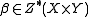 be cycles such that
be cycles such that 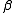 intersects
intersects 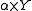 properly. If
properly. If  ~X 0, then
~X 0, then  ~Y 0, where
~Y 0, where 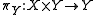 is the projection.
is the projection.
The push-forward cycle in the last axiom is often denoted
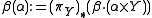
If
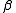 is the graph of a function, then this reduces to the push-forward of the function. The generalizations of functions from X to Y to cycles on X × Y are known as correspondences
is the graph of a function, then this reduces to the push-forward of the function. The generalizations of functions from X to Y to cycles on X × Y are known as correspondencesCorrespondence (mathematics)
In mathematics and mathematical economics, correspondence is a term with several related but not identical meanings.* In general mathematics, correspondence is an alternative term for a relation between two sets...
. The last axiom allows us to push forward cycles by a correspondence.
Examples of equivalence relations
The most common equivalence relations, listed from strongest to weakest, are gathered below in a table.| definition | remarks | |
|---|---|---|
| rational equivalence | Z ∼rat Z' if there is a cycle V on X × P1 Projective line In mathematics, a projective line is a one-dimensional projective space. The projective line over a field K, denoted P1, may be defined as the set of one-dimensional subspaces of the two-dimensional vector space K2 .For the generalisation to the projective line over an associative ring, see... flat Flat morphism In mathematics, in particular in the theory of schemes in algebraic geometry, a flat morphism f from a scheme X to a scheme Y is a morphism such that the induced map on every stalk is a flat map of rings, i.e.,is a flat map for all P in X... over P1, such that V ∩ X × {0} = Z and V ∩ X × {∞} = Z' . |
the finest adequate equivalence relation. "∩" denotes intersection in the cycle-theoretic sense (i.e. with multiplicities). see also Chow ring Chow ring In algebraic geometry, the Chow ring of an algebraic variety is an algebraic-geometric analogue of the cohomology ring of the variety considered as a topological space: its elements are formed out of actual subvarieties and its multiplicative structure is derived from the intersection of... |
| algebraic equivalence | Z ∼alg Z' if there is a curve Curve In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight... C and a cycle V on X × C flat over C, such that V ∩ X × {c} = Z and V ∩ X × {d} = Z' for two points c and d on the curve. |
strictly stronger than homological equivalence, see also Néron–Severi group Néron–Severi group In algebraic geometry, the Néron–Severi group of a variety isthe group of divisors modulo algebraic equivalence; in other words it is the group of components of the Picard scheme of a variety. Its rank is called the Picard number... |
| smash-nilpotence equivalence | Z ∼sn Z' if Z - Z' is smash-nilpotent on X, that is, if 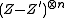 ∼rat 0 on Xn for n >> 0. ∼rat 0 on Xn for n >> 0. |
introduced by Voevodsky in 1995. |
| homological equivalence | for a given Weil cohomology Weil cohomology theory In algebraic geometry, a Weil cohomology or Weil cohomology theory is a cohomology satisfying certain axioms concerning the interplay of algebraic cycles and cohomology groups. The name is in honor of André Weil... H, Z ∼hom Z' if the image of the cycles under the cycle class map agrees |
depends a priori of the choice of H, but does not assuming the standard conjecture Standard conjectures on algebraic cycles In mathematics, the standard conjectures about algebraic cycles is a package of several conjectures describing the relationship of algebraic cycles and Weil cohomology theories. One of the original applications of these conjectures, envisaged by Alexander Grothendieck, was to prove that his... D |
| numerical equivalence | Z ∼num Z' if Z ∩ T = Z' ∩ T, where T is any cycle such that dim T = codim Z (so that the intersection is a linear combination of points) | the coarsest equivalence relation |

