Abrikosov vortex
Encyclopedia
In superconductivity, an Abrikosov vortex is a vortex of supercurrent
in a type-II superconductor
. The supercurrent
circulates around the normal (i.e. non-superconducting) core of the vortex. The core has a size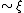
— the superconducting coherence length
(parameter of a Ginzburg-Landau theory
). The supercurrents decay on the distance about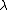
(London penetration depth
) from the core. Note that in type-II superconductors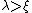
. The circulating supercurrent
s induce magnetic fields with the total flux equal to a single flux quantum
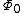. Therefore, an Abrikosov vortex is often called a fluxon
.
The magnetic field distribution of a single vortex far from its core can be described by
where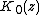
is a zeroth-order Bessel function
. Note that, according to the above formula, at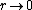
the magnetic field 
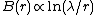, i.e. logarithmically diverges. In reality, for 
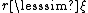the field is simply given by
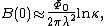
where κ = λ/ξ is known as the Ginzburg-Landau parameter, which must be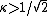
in type-II superconductor
s.
Abrikosov vortices can be trapped in a type-II superconductor
by chance, on defects, etc. Even if initially type-II superconductor
contains no vortices, and one applies a magnetic field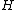
larger than the lower critical field 
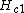(but smaller than the upper critical field
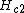), the field penetrates into superconductor in terms of Abrikosov vortices. Each vortex carries one thread of magnetic field with the flux 
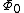. Abrikosov vortices form a lattice (usually triangular, may be with defects/dislocations) with the average vortex density (flux density) approximately equal to the externally applied magnetic field.
Supercurrent
A supercurrent is a superconducting current, that is, electric current which flows without dissipation....
in a type-II superconductor
Type-II superconductor
A Type-II superconductor is a superconductor characterized by the formation of vortex lattices in magnetic field. It has a continuous second order phase transition from the superconducting to the normal state within an increasing magnetic field....
. The supercurrent
Supercurrent
A supercurrent is a superconducting current, that is, electric current which flows without dissipation....
circulates around the normal (i.e. non-superconducting) core of the vortex. The core has a size
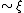— the superconducting coherence lengthSuperconducting coherence length
A Superconducting coherence length, usually denoted as \xi, can be interpreted in two different ways:* It gives approximate spatial dimension of the Cooper pair,...
(parameter of a Ginzburg-Landau theory
Ginzburg-Landau theory
In physics, Ginzburg–Landau theory, named after Vitaly Lazarevich Ginzburg and Lev Landau, is a mathematical theory used to model superconductivity. It does not purport to explain the microscopic mechanisms giving rise to superconductivity...
). The supercurrents decay on the distance about
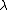(London penetration depthLondon penetration depth
In superconductors, the London penetration depth characterizes the distance to which a magnetic field penetrates into a superconductor and becomes equal to 1/e times that of the magnetic field at the surface of the superconductor...
) from the core. Note that in type-II superconductors
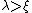. The circulating supercurrentSupercurrent
A supercurrent is a superconducting current, that is, electric current which flows without dissipation....
s induce magnetic fields with the total flux equal to a single flux quantum
Magnetic flux quantum
The magnetic flux quantum Φ0 is the quantum of magnetic flux passing through a superconductor. The phenomenon of flux quantization was discovered B. S. Deaver and W. M. Fairbank and, independently, by R. Doll and M. Nabauer, in 1961...
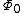. Therefore, an Abrikosov vortex is often called a fluxonFluxon
In physics, a fluxon is a quantum of electromagnetic flux. The term may have any of several related meanings.- Superconductivity :In the context of superconductivity, a fluxon is a small whisker of normal phase surrounded by superconducting phase. Supercurrents circulate around its center...
.
The magnetic field distribution of a single vortex far from its core can be described by
where
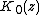is a zeroth-order Bessel functionBessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
. Note that, according to the above formula, at
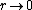the magnetic field 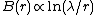, i.e. logarithmically diverges. In reality, for 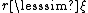the field is simply given by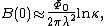where κ = λ/ξ is known as the Ginzburg-Landau parameter, which must be
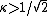in type-II superconductorType-II superconductor
A Type-II superconductor is a superconductor characterized by the formation of vortex lattices in magnetic field. It has a continuous second order phase transition from the superconducting to the normal state within an increasing magnetic field....
s.
Abrikosov vortices can be trapped in a type-II superconductor
Type-II superconductor
A Type-II superconductor is a superconductor characterized by the formation of vortex lattices in magnetic field. It has a continuous second order phase transition from the superconducting to the normal state within an increasing magnetic field....
by chance, on defects, etc. Even if initially type-II superconductor
Type-II superconductor
A Type-II superconductor is a superconductor characterized by the formation of vortex lattices in magnetic field. It has a continuous second order phase transition from the superconducting to the normal state within an increasing magnetic field....
contains no vortices, and one applies a magnetic field
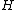larger than the lower critical field 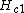(but smaller than the upper critical fieldUpper critical field
-Upper critical field:The upper critical field is the magnetic field which completely suppresses superconductivity in a Type II superconductor at 0K ....
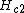), the field penetrates into superconductor in terms of Abrikosov vortices. Each vortex carries one thread of magnetic field with the flux 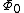. Abrikosov vortices form a lattice (usually triangular, may be with defects/dislocations) with the average vortex density (flux density) approximately equal to the externally applied magnetic field.See also
- Ginzburg-Landau theoryGinzburg-Landau theoryIn physics, Ginzburg–Landau theory, named after Vitaly Lazarevich Ginzburg and Lev Landau, is a mathematical theory used to model superconductivity. It does not purport to explain the microscopic mechanisms giving rise to superconductivity...
- Type-II superconductorType-II superconductorA Type-II superconductor is a superconductor characterized by the formation of vortex lattices in magnetic field. It has a continuous second order phase transition from the superconducting to the normal state within an increasing magnetic field....
- Alexei Alexeyevich AbrikosovAlexei Alexeyevich AbrikosovAlexei Alexeyevich Abrikosov is a Soviet and Russian theoretical physicist whose main contributions are in the field of condensed matter physics. He was awarded the Nobel Prize in Physics in 2003.- Biography :...
- Pinning forcePinning forcePinning force is a force acting on a pinned object from a pinning center. In solid state physics, this most often refers to the vortex pinning, the pinning of the magnetic vortices by different kinds of the defects in a type II superconductor...
- Flux pinningFlux pinningFlux pinning is the phenomenon that magnetic flux lines do not move in spite of the Lorentz force acting on them inside a current-carrying...