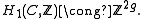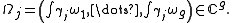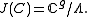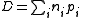Abel–Jacobi map
Encyclopedia
In mathematics
, the Abel–Jacobi map is a construction of algebraic geometry
which relates an algebraic curve
to its Jacobian variety
. In Riemannian geometry
, it is a more general construction mapping a manifold
to its Jacobi torus.
The name derives from the theorem of Abel
and Jacobi that two effective divisors are linearly equivalent if and only if they are indistinguishable under the Abel–Jacobi map.
Geometrically, this homology group consists of (homology classes of) cycles in C, or in other words, closed loops. Therefore we can choose 2g loops generating it. On the other hand, another, more algebro-geometric way of saying that the genus of C is g, is that
generating it. On the other hand, another, more algebro-geometric way of saying that the genus of C is g, is that
By definition, this is the space of globally defined differential form
s on C, so we can choose g linearly independent forms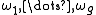 . Given forms and closed loops we can integrate, and we define 2g vectors
. Given forms and closed loops we can integrate, and we define 2g vectors
It follows from the Riemann bilinear relations that the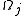 generate a nondegenerate lattice
generate a nondegenerate lattice
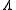 (that is, they are a real basis for
(that is, they are a real basis for 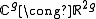 ), and the Jacobian is defined by
), and the Jacobian is defined by
The Abel–Jacobi map is then defined as follows. We pick some base point and, nearly mimicking the definition of
and, nearly mimicking the definition of 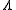 , define the map
, define the map
Although this is seemingly dependent on a path from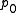 to
to  any two such paths define a closed loop in
any two such paths define a closed loop in  and, therefore, an element of
and, therefore, an element of 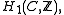 so integration over it gives an element of
so integration over it gives an element of 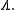 Thus the difference is erased in the passage to the quotient by
Thus the difference is erased in the passage to the quotient by 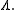 . Changing base-point
. Changing base-point 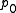 does change the map, but only by a translation of the torus.
does change the map, but only by a translation of the torus.
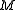 be a smooth compact manifold
be a smooth compact manifold
. Let be its fundamental group. Let
be its fundamental group. Let  be its abelianisation map. Let
be its abelianisation map. Let
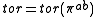 be the torsion subgroup of
be the torsion subgroup of
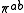 . Let
. Let 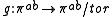
be the quotient by torsion. If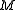 is a surface,
is a surface, 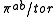 is non-canonically isomorphic to
is non-canonically isomorphic to
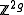 , where
, where  is the genus; more generally,
is the genus; more generally,  is non-canonically isomorphic to
is non-canonically isomorphic to 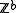 , where
, where 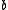 is the first Betti number. Let
is the first Betti number. Let 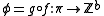 be the composite homomorphism.
be the composite homomorphism.
Definition. The cover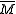 of the manifold
of the manifold
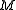 corresponding the subgroup
corresponding the subgroup 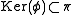 is called the universal (or maximal) free abelian
is called the universal (or maximal) free abelian
cover.
Now assume M has a Riemannian metric. Let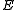 be the space of harmonic
be the space of harmonic 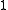 -forms on
-forms on
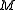 , with dual
, with dual 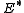 canonically identified with
canonically identified with
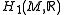 . By integrating an integral
. By integrating an integral
harmonic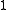 -form along paths from a basepoint
-form along paths from a basepoint 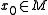 , we obtain a map to the circle
, we obtain a map to the circle
 .
.
Similarly, in order to define a map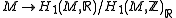 without choosing a basis for
without choosing a basis for
cohomology, we argue as follows. Let be a point in the
be a point in the
universal cover of
of 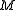 . Thus
. Thus
 is represented by a point of
is represented by a point of  together
together
with a path from
from 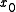 to it. By
to it. By
integrating along the path , we obtain a linear form,
, we obtain a linear form,
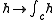 , on
, on 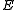 . We thus obtain a map
. We thus obtain a map
 , which,
, which,
furthermore, descends to a map
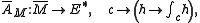
where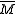 is the universal free abelian cover.
is the universal free abelian cover.
Definition. The Jacobi variety (Jacobi torus) of is the
is the
torus
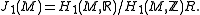
Definition. The Abel–Jacobi map

is obtained from the map above by passing to quotients.
The Abel–Jacobi map is unique up to translations of the Jacobi torus. The map has applications in Systolic geometry.
is a divisor (meaning a formal integer-linear combination of points of C). We can define
and therefore speak of the value of the Abel–Jacobi map on divisors. The theorem is then that if D and E are two effective divisors, meaning that the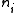 are all positive integers, then
are all positive integers, then
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Abel–Jacobi map is a construction of algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
which relates an algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
to its Jacobian variety
Jacobian variety
In mathematics, the Jacobian variety J of a non-singular algebraic curve C of genus g is the moduli space of degree 0 line bundles...
. In Riemannian geometry
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
, it is a more general construction mapping a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
to its Jacobi torus.
The name derives from the theorem of Abel
Niels Henrik Abel
Niels Henrik Abel was a Norwegian mathematician who proved the impossibility of solving the quintic equation in radicals.-Early life:...
and Jacobi that two effective divisors are linearly equivalent if and only if they are indistinguishable under the Abel–Jacobi map.
Construction of the map
In complex algebraic geometry, the Jacobian of a curve C is constructed using path integration. Namely, suppose C has genus g, which means topologically thatGeometrically, this homology group consists of (homology classes of) cycles in C, or in other words, closed loops. Therefore we can choose 2g loops
 generating it. On the other hand, another, more algebro-geometric way of saying that the genus of C is g, is that
generating it. On the other hand, another, more algebro-geometric way of saying that the genus of C is g, is that
-
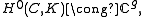 where K is the canonical bundleCanonical bundleIn mathematics, the canonical bundle of a non-singular algebraic variety V of dimension n is the line bundle\,\!\Omega^n = \omegawhich is the nth exterior power of the cotangent bundle Ω on V. Over the complex numbers, it is the determinant bundle of holomorphic n-forms on V.This is the dualising...
where K is the canonical bundleCanonical bundleIn mathematics, the canonical bundle of a non-singular algebraic variety V of dimension n is the line bundle\,\!\Omega^n = \omegawhich is the nth exterior power of the cotangent bundle Ω on V. Over the complex numbers, it is the determinant bundle of holomorphic n-forms on V.This is the dualising...
on C.
By definition, this is the space of globally defined differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s on C, so we can choose g linearly independent forms
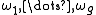 . Given forms and closed loops we can integrate, and we define 2g vectors
. Given forms and closed loops we can integrate, and we define 2g vectors
It follows from the Riemann bilinear relations that the
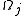 generate a nondegenerate lattice
generate a nondegenerate latticeLattice (group)
In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
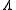 (that is, they are a real basis for
(that is, they are a real basis for 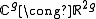 ), and the Jacobian is defined by
), and the Jacobian is defined by
The Abel–Jacobi map is then defined as follows. We pick some base point
 and, nearly mimicking the definition of
and, nearly mimicking the definition of 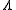 , define the map
, define the map
Although this is seemingly dependent on a path from
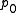 to
to  any two such paths define a closed loop in
any two such paths define a closed loop in  and, therefore, an element of
and, therefore, an element of 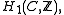 so integration over it gives an element of
so integration over it gives an element of 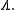 Thus the difference is erased in the passage to the quotient by
Thus the difference is erased in the passage to the quotient by 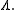 . Changing base-point
. Changing base-point 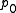 does change the map, but only by a translation of the torus.
does change the map, but only by a translation of the torus.Invariant construction of the Abel–Jacobi map
Let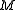 be a smooth compact manifold
be a smooth compact manifoldManifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
. Let
 be its fundamental group. Let
be its fundamental group. Let  be its abelianisation map. Let
be its abelianisation map. Let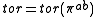 be the torsion subgroup of
be the torsion subgroup of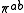 . Let
. Let 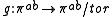
be the quotient by torsion. If
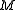 is a surface,
is a surface, 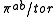 is non-canonically isomorphic to
is non-canonically isomorphic to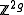 , where
, where  is the genus; more generally,
is the genus; more generally,  is non-canonically isomorphic to
is non-canonically isomorphic to 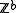 , where
, where 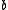 is the first Betti number. Let
is the first Betti number. Let 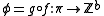 be the composite homomorphism.
be the composite homomorphism.Definition. The cover
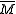 of the manifold
of the manifold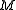 corresponding the subgroup
corresponding the subgroup 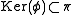 is called the universal (or maximal) free abelian
is called the universal (or maximal) free abeliancover.
Now assume M has a Riemannian metric. Let
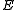 be the space of harmonic
be the space of harmonic 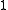 -forms on
-forms on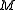 , with dual
, with dual 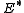 canonically identified with
canonically identified with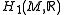 . By integrating an integral
. By integrating an integralharmonic
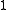 -form along paths from a basepoint
-form along paths from a basepoint 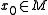 , we obtain a map to the circle
, we obtain a map to the circle .
.Similarly, in order to define a map
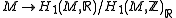 without choosing a basis for
without choosing a basis forcohomology, we argue as follows. Let
 be a point in the
be a point in theuniversal cover
 of
of 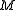 . Thus
. Thus is represented by a point of
is represented by a point of  together
togetherwith a path
 from
from 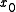 to it. By
to it. Byintegrating along the path
 , we obtain a linear form,
, we obtain a linear form,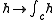 , on
, on 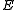 . We thus obtain a map
. We thus obtain a map , which,
, which,furthermore, descends to a map
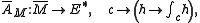
where
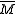 is the universal free abelian cover.
is the universal free abelian cover.Definition. The Jacobi variety (Jacobi torus) of
 is the
is thetorus
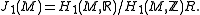
Definition. The Abel–Jacobi map

is obtained from the map above by passing to quotients.
The Abel–Jacobi map is unique up to translations of the Jacobi torus. The map has applications in Systolic geometry.
Abel–Jacobi theorem
The following theorem was proved by Abel and Jacobi (each one proved one implication): Suppose thatis a divisor (meaning a formal integer-linear combination of points of C). We can define
and therefore speak of the value of the Abel–Jacobi map on divisors. The theorem is then that if D and E are two effective divisors, meaning that the
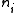 are all positive integers, then
are all positive integers, then
-
 if and only if
if and only if  is linearly equivalent to
is linearly equivalent to 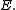 This implies that the Abel–Jacobi map induces an isomorphism (of abelian groups) between the space of divisor classes of degree zero and the Jacobian.
This implies that the Abel–Jacobi map induces an isomorphism (of abelian groups) between the space of divisor classes of degree zero and the Jacobian.