
Zariski ring
Encyclopedia
In commutative algebra
, a Zariski ring, introduced by , is a commutative Noetherian
topological ring A whose topology is defined by an ideal m contained in the Jacobson radical
, the intersection of all maximal ideals. Examples of Zariski rings are notherian local rings and -adic completions of notherian rings.
-adic completions of notherian rings.
Let A be a noetherian ring and its
its  -adic completion. Then the following are equivalent.
-adic completion. Then the following are equivalent.
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
, a Zariski ring, introduced by , is a commutative Noetherian
Noetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
topological ring A whose topology is defined by an ideal m contained in the Jacobson radical
Jacobson radical
In mathematics, more specifically ring theory, a branch of abstract algebra, the Jacobson radical of a ring R is an ideal which consists of those elements in R which annihilate all simple right R-modules. It happens that substituting "left" in place of "right" in the definition yields the same...
, the intersection of all maximal ideals. Examples of Zariski rings are notherian local rings and
 -adic completions of notherian rings.
-adic completions of notherian rings.Let A be a noetherian ring and
 its
its  -adic completion. Then the following are equivalent.
-adic completion. Then the following are equivalent.
-
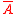 is faithfully flat over A (in general, only flat over it).
is faithfully flat over A (in general, only flat over it). - Every maximal ideal is closed for the
 -adic topology.
-adic topology. - A is a Zariski ring.

