Young measure
Encyclopedia
In mathematical analysis
, a Young measure is a parameterized measure
that is associated with certain subsequences of a given bounded sequence of measurable functions. Young measures have applications in the calculus of variations
and the study of nonlinear partial differential equations. They are named after Laurence Chisholm Young
.
be a bounded sequence in 
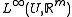, where 
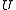denotes an open bounded subset of 
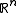. Then there exists a subsequence 
and for almost every 
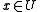a Borel probability measure 
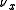on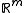 
such that for each 
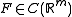we have 
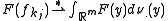in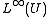 
. The measures 
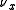are called the Young measures generated by the sequence 
.
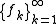subject to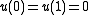 
generates the Young measures 
.
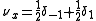This captures the essential features of all minimizing sequences to this problem, namely developing finer and finer slopes of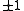
.
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, a Young measure is a parameterized measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
that is associated with certain subsequences of a given bounded sequence of measurable functions. Young measures have applications in the calculus of variations
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
and the study of nonlinear partial differential equations. They are named after Laurence Chisholm Young
Laurence Chisholm Young
Laurence Chisholm Young was a mathematician known for his contributions to measure theory, the calculus of variations, optimal control theory, and potential theory...
.
Definition
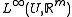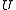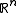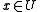We let be a bounded sequence in , where denotes an open bounded subset of . Then there exists a subsequence and for almost every a Borel probability measure 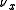on 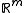such that for each 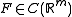we have 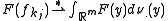in 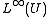. The measures 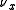are called the Young measures generated by the sequence 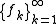.Example
Every minimizing sequence of subject to 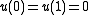generates the Young measures 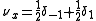.This captures the essential features of all minimizing sequences to this problem, namely developing finer and finer slopes of
.
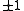