Worm-like chain
Encyclopedia
The worm-like chain model in polymer physics
is used to describe the behavior of semi-flexible polymers; it is sometimes referred to as the Kratky
-Porod
model.
model that is flexible only between discrete segments. The worm-like chain model is particularly suited for describing stiffer polymers, with successive segments displaying a sort of cooperativity: all pointing in roughly the same direction. At room temperature, the polymer adopts a conformational ensemble that is smoothly curved; at
K, the polymer adopts a rigid rod conformation.
For a polymer of length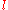
, parametrize the path of the polymer as 
, allow 
to be the unit tangent vector to the chain at 
, and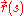 
to be the position vector along the chain. Then
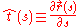and the end-to-end distance 
.
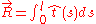It can be shown that the orientation correlation function
for a worm-like chain follows an exponential decay:
,
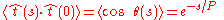where
is by definition the polymer's characteristic persistence length
. A useful value is the mean square end-to-end distance of the polymer:
Several biologically important polymers can be effectively modeled as worm-like chains, including:
Laboratory tools such as atomic force microscopy (AFM) and optical tweezers
have been used to characterize the force-dependent stretching behavior of the polymers listed above. An interpolation formula that describes the extension
of a WLC with contour length 
and persistence length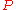 
in response to a stretching force 
is
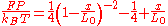
where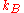
is the Boltzmann constant and 
is the absolute temperature (Bustamante, et al., 1994; Marko et al., 1995).
In the particular case of stretching DNA in physiological buffer (near neutral pH, ionic strength approximately 100 mM) at room temperature, the compliance of the DNA along the contour must be accounted for. This enthalpic compliance is accounted for by adding a stretch modulus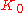
to the above relation:
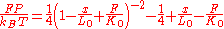
where a typical value for the stretch modulus of double-stranded DNA is around 1000 pN and 45 nm for the persistence length (Wang, et al., 1997).
Polymer physics
Polymer physics is the field of physics that studies polymers, their fluctuations, mechanical properties, as well as the kinetics of reactions involving degradation and polymerisation of polymers and monomers respectively....
is used to describe the behavior of semi-flexible polymers; it is sometimes referred to as the Kratky
Otto Kratky
Otto Kratky was an Austrian physicist. He is best known for his contribution to the small-angle X-ray scattering method and for the Kratky plot...
-Porod
Günther Porod
Günther Porod was an Austrian physicist. He is best known for his work on the small-angle X-ray scattering method, done in collaboration with his teacher Otto Kratky...
model.
Theoretical Considerations
The WLC model envisions an isotropic rod that is continuously flexible; this is in contrast to the freely-jointed chainIdeal chain
An ideal chain is the simplest model to describe a polymer. It only assumes a polymer as a random walk and neglects any kind of interactions among monomers...
model that is flexible only between discrete segments. The worm-like chain model is particularly suited for describing stiffer polymers, with successive segments displaying a sort of cooperativity: all pointing in roughly the same direction. At room temperature, the polymer adopts a conformational ensemble that is smoothly curved; at
K, the polymer adopts a rigid rod conformation.For a polymer of length
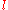, parametrize the path of the polymer as , allow to be the unit tangent vector to the chain at , and 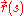to be the position vector along the chain. Then 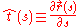and the end-to-end distance 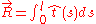.It can be shown that the orientation correlation function
Correlation function
A correlation function is the correlation between random variables at two different points in space or time, usually as a function of the spatial or temporal distance between the points...
for a worm-like chain follows an exponential decay:
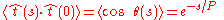,where
is by definition the polymer's characteristic persistence lengthPersistence length
The persistence length is a basic mechanical property quantifying the stiffness of a polymer or of a string.Informally, for pieces of the polymer that are shorter than the persistence length, the molecule behaves rather like a flexible elastic rod, while for pieces of the polymer that are much...
. A useful value is the mean square end-to-end distance of the polymer:
- Note that in the limit of
, then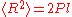 
. This can be used to show that a Kuhn segmentKuhn lengthThe Kuhn length is a theoretical treatment, developed by Werner Kuhn, in which a real polymer chain is considered as a collection of N Kuhn segments each with a Kuhn length b. Each Kuhn segment can be thought of as if they are freely jointed with each other...
is equal to twice the persistence length of a worm-like chain.
Biological Relevance
Several biologically important polymers can be effectively modeled as worm-like chains, including:
- double-stranded DNADNADeoxyribonucleic acid is a nucleic acid that contains the genetic instructions used in the development and functioning of all known living organisms . The DNA segments that carry this genetic information are called genes, but other DNA sequences have structural purposes, or are involved in...
and RNARNARibonucleic acid , or RNA, is one of the three major macromolecules that are essential for all known forms of life....
; - unstructured RNARNARibonucleic acid , or RNA, is one of the three major macromolecules that are essential for all known forms of life....
; - unstructured polypeptides (proteins).
Stretching Worm-like Chain Polymers
Laboratory tools such as atomic force microscopy (AFM) and optical tweezers
Optical tweezers
Optical tweezers are scientific instruments that use a highly focused laser beam to provide an attractive or repulsive force , depending on the refractive index mismatch to physically hold and move microscopic dielectric objects...
have been used to characterize the force-dependent stretching behavior of the polymers listed above. An interpolation formula that describes the extension
of a WLC with contour length and persistence length 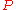in response to a stretching force is 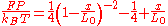where
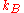is the Boltzmann constant and is the absolute temperature (Bustamante, et al., 1994; Marko et al., 1995).In the particular case of stretching DNA in physiological buffer (near neutral pH, ionic strength approximately 100 mM) at room temperature, the compliance of the DNA along the contour must be accounted for. This enthalpic compliance is accounted for by adding a stretch modulus
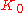to the above relation: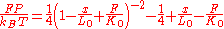where a typical value for the stretch modulus of double-stranded DNA is around 1000 pN and 45 nm for the persistence length (Wang, et al., 1997).