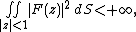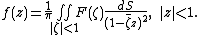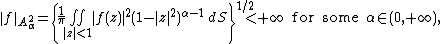Wirtinger's representation and projection theorem
Encyclopedia
In mathematics, Wirtinger's representation and projection theorem is a theorem
proved by Wilhelm Wirtinger
in 1932 in connection with some problems of approximation theory
. This theorem gives the representation formula for the holomorphic subspace
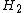 of the simple, unweighted holomorphic Hilbert space
of the simple, unweighted holomorphic Hilbert space
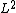 of functions square-integrable over the surface of the unit disc
of functions square-integrable over the surface of the unit disc 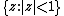 of the complex plane
of the complex plane
, along with a form of the orthogonal projection from to
to 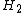 .
.
Wirtinger's paper contains the following theorem presented also in J. L. Walsh's well-known monograph
(p. 150) with a different proof. If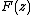 is of the class
is of the class 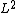 on
on  , i.e.
, i.e.
where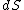 is the area element, then the unique function
is the area element, then the unique function 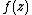 of the holomorphic subclass
of the holomorphic subclass  , such that
, such that
is least, is given by
The last formula gives a form for the orthogonal projection from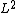 to
to 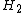 . Besides, replacement of
. Besides, replacement of 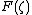 by
by 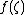 makes it Wirtinger's representation for all
makes it Wirtinger's representation for all 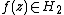 . This is an analog of the well-known Cauchy integral formula with the square of the Cauchy kernel. Later, after 1950s, a degree of the Cauchy kernel was called reproducing kernel, and the notation
. This is an analog of the well-known Cauchy integral formula with the square of the Cauchy kernel. Later, after 1950s, a degree of the Cauchy kernel was called reproducing kernel, and the notation 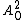 became common for the class
became common for the class 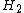 .
.
In 1948 Mkhitar Djrbashian
extended Wirtinger's representation and projection to the wider, weighted Hilbert spaces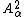 of functions
of functions 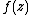 holomorphic in
holomorphic in 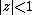 , which satisfy the condition
, which satisfy the condition
and also to some Hilbert spaces of entire functions. The extensions of these results to some weighted spaces of functions holomorphic in
spaces of functions holomorphic in 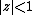 and similar spaces of entire functions, the unions of which respectively coincide with all functions holomorphic in
and similar spaces of entire functions, the unions of which respectively coincide with all functions holomorphic in 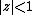 and the whole set of entire functions can be seen in .
and the whole set of entire functions can be seen in .
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
proved by Wilhelm Wirtinger
Wilhelm Wirtinger
Wilhelm Wirtinger was an Austrian mathematician, working in complex analysis, geometry, algebra, number theory, Lie groups and knot theory.-Biography:...
in 1932 in connection with some problems of approximation theory
Approximation theory
In mathematics, approximation theory is concerned with how functions can best be approximated with simpler functions, and with quantitatively characterizing the errors introduced thereby...
. This theorem gives the representation formula for the holomorphic subspace
Linear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
 of the simple, unweighted holomorphic Hilbert space
of the simple, unweighted holomorphic Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
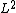 of functions square-integrable over the surface of the unit disc
of functions square-integrable over the surface of the unit disc 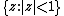 of the complex plane
of the complex planeComplex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
, along with a form of the orthogonal projection from
 to
to 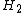 .
.Wirtinger's paper contains the following theorem presented also in J. L. Walsh's well-known monograph
(p. 150) with a different proof. If
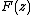 is of the class
is of the class 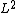 on
on  , i.e.
, i.e.where
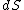 is the area element, then the unique function
is the area element, then the unique function 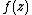 of the holomorphic subclass
of the holomorphic subclass  , such that
, such thatis least, is given by
The last formula gives a form for the orthogonal projection from
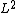 to
to 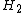 . Besides, replacement of
. Besides, replacement of 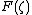 by
by 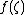 makes it Wirtinger's representation for all
makes it Wirtinger's representation for all 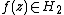 . This is an analog of the well-known Cauchy integral formula with the square of the Cauchy kernel. Later, after 1950s, a degree of the Cauchy kernel was called reproducing kernel, and the notation
. This is an analog of the well-known Cauchy integral formula with the square of the Cauchy kernel. Later, after 1950s, a degree of the Cauchy kernel was called reproducing kernel, and the notation 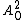 became common for the class
became common for the class 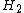 .
.In 1948 Mkhitar Djrbashian
Mkhitar Djrbashian
Mkhitar Djrbashian was a notable Armenian...
extended Wirtinger's representation and projection to the wider, weighted Hilbert spaces
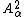 of functions
of functions 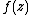 holomorphic in
holomorphic in 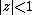 , which satisfy the condition
, which satisfy the conditionand also to some Hilbert spaces of entire functions. The extensions of these results to some weighted
 spaces of functions holomorphic in
spaces of functions holomorphic in 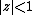 and similar spaces of entire functions, the unions of which respectively coincide with all functions holomorphic in
and similar spaces of entire functions, the unions of which respectively coincide with all functions holomorphic in 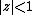 and the whole set of entire functions can be seen in .
and the whole set of entire functions can be seen in .