
Weighted matroid
Encyclopedia
In combinatorics
, a branch of mathematics
, a weighted matroid is a matroid
endowed with function with respect to which one can perform a greedy algorithm
.
A weight function w : E → R+ for a matroid M=(E, I) assigns a strictly positive weight to each element of E. We extend the function to subsets of E by summation; w(A) is the sum of w(x) over x in A. A matroid with an associated weight function is called a weighted matroid.
of a graph. That is, given a graph and a weight for each edge, find a forest containing every vertex and maximizing the total weight of the edges in the tree. This problem arises in some clustering applications. If we look at the definition of the forest matroid above, we see that the maximum spanning forest is simply the independent set with largest total weight — such a set must span the graph, for otherwise we can add edges without creating cycles. But how do we find it?
The result is clearly an independent set. It is a maximal independent set because if B U {x} is not independent for some subset B of A, then A U {x} is not independent either (the contrapositive follows from the hereditary property). Thus if we pass up an element, we'll never have an opportunity to use it later. We will generalize this algorithm to solve a harder problem.
for computing an optimal set of a weighted matroid. It works as follows:
This algorithm finds a basis, since it is a special case of the above algorithm. It always chooses the element of largest weight that it can while preserving independence (thus the term "greedy"). This always produces an optimal set: suppose that it produces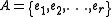 and that
and that 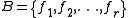 . Now for any
. Now for any 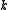 with
with 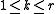 , consider open sets
, consider open sets 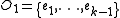 and
and 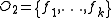 . Since
. Since 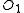 is smaller than
is smaller than 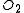 , there is some element of
, there is some element of 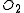 which can be put into
which can be put into 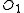 with the result still being independent. However
with the result still being independent. However 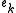 is an element of maximal weight that can be added to
is an element of maximal weight that can be added to 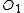 to maintain independence. Thus
to maintain independence. Thus 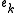 is of no smaller weight than some element of
is of no smaller weight than some element of 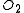 , and hence
, and hence 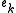 is of at least a large a weight as
is of at least a large a weight as 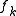 . As this is true for all
. As this is true for all  ,
, 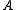 is weightier than
is weightier than  .
.
. We also need to test for each x whether A U {x} is independent; assuming independence tests require O(f(|E|)) time, the total time for the algorithm is O(|E|log|E| + |E|f(|E|)).
If we want to find a minimum spanning tree instead, we simply "invert" the weight function by subtracting it from a large constant. More specifically, let wmin(x) = W - w(x), where W exceeds the total weight over all graph edges. Many more optimization problems about all sorts of matroids and weight functions can be solved in this trivial way, although in many cases more efficient algorithms can be found that exploit more specialized properties.
 of "independent" sets which is a down-set but not a matroid, then the greedy algorithm will not always work. For then there are independent sets
of "independent" sets which is a down-set but not a matroid, then the greedy algorithm will not always work. For then there are independent sets 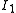 and
and 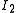 with
with  , but such that for no
, but such that for no 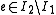 is
is 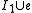 independent.
independent.
Pick an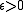 and
and  such that
such that  . Weight the elements of
. Weight the elements of  in the range
in the range 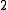 to
to 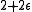 , the elements of
, the elements of 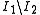 in the range
in the range  to
to  , the elements of
, the elements of 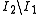 in the range
in the range 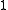 to
to 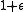 , and the rest in the range
, and the rest in the range 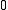 to
to  . The greedy algorithm will select the elements of
. The greedy algorithm will select the elements of 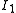 , and then cannot pick any elements of
, and then cannot pick any elements of  . Therefore the independent set it constructs will be of weight at most
. Therefore the independent set it constructs will be of weight at most  , which is smaller than the weight of
, which is smaller than the weight of  .
.
connected weighted matroids to greedy algorithms in his paper "Matroids and the greedy algorithm". Korte and Lovász would generalize these ideas to objects called greedoid
s, which allow even larger classes of problems to be solved by greedy algorithms.
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a weighted matroid is a matroid
Matroid
In combinatorics, a branch of mathematics, a matroid or independence structure is a structure that captures the essence of a notion of "independence" that generalizes linear independence in vector spaces....
endowed with function with respect to which one can perform a greedy algorithm
Greedy algorithm
A greedy algorithm is any algorithm that follows the problem solving heuristic of making the locally optimal choice at each stagewith the hope of finding the global optimum....
.
A weight function w : E → R+ for a matroid M=(E, I) assigns a strictly positive weight to each element of E. We extend the function to subsets of E by summation; w(A) is the sum of w(x) over x in A. A matroid with an associated weight function is called a weighted matroid.
Spanning forest algorithms
As a simple example, say we wish to find the maximum spanning forestSpanning tree (mathematics)
In the mathematical field of graph theory, a spanning tree T of a connected, undirected graph G is a tree composed of all the vertices and some of the edges of G. Informally, a spanning tree of G is a selection of edges of G that form a tree spanning every vertex...
of a graph. That is, given a graph and a weight for each edge, find a forest containing every vertex and maximizing the total weight of the edges in the tree. This problem arises in some clustering applications. If we look at the definition of the forest matroid above, we see that the maximum spanning forest is simply the independent set with largest total weight — such a set must span the graph, for otherwise we can add edges without creating cycles. But how do we find it?
Finding a basis
There is a simple algorithm for finding a basis:- Initially let A be the empty set.
- For each x in E
- if A U {x} is independent, then set A to A U {x}.
The result is clearly an independent set. It is a maximal independent set because if B U {x} is not independent for some subset B of A, then A U {x} is not independent either (the contrapositive follows from the hereditary property). Thus if we pass up an element, we'll never have an opportunity to use it later. We will generalize this algorithm to solve a harder problem.
Extension to optimal
An independent set of largest total weight is called an optimal set. Optimal sets are always bases, because if an edge can be added, it should be; this only increases the total weight. As it turns out, there is a trivial greedy algorithmGreedy algorithm
A greedy algorithm is any algorithm that follows the problem solving heuristic of making the locally optimal choice at each stagewith the hope of finding the global optimum....
for computing an optimal set of a weighted matroid. It works as follows:
- Initially let A be the empty set.
- For each x in E, taken in (monotonically) decreasing order by weight
- if A U {x} is independent, then set A to A U {x}.
This algorithm finds a basis, since it is a special case of the above algorithm. It always chooses the element of largest weight that it can while preserving independence (thus the term "greedy"). This always produces an optimal set: suppose that it produces
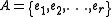 and that
and that 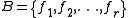 . Now for any
. Now for any 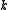 with
with 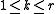 , consider open sets
, consider open sets 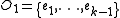 and
and 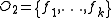 . Since
. Since 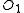 is smaller than
is smaller than 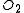 , there is some element of
, there is some element of 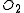 which can be put into
which can be put into 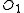 with the result still being independent. However
with the result still being independent. However 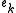 is an element of maximal weight that can be added to
is an element of maximal weight that can be added to 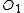 to maintain independence. Thus
to maintain independence. Thus 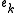 is of no smaller weight than some element of
is of no smaller weight than some element of 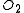 , and hence
, and hence 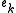 is of at least a large a weight as
is of at least a large a weight as 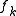 . As this is true for all
. As this is true for all  ,
, 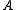 is weightier than
is weightier than  .
.Complexity analysis
The easiest way to traverse the members of E in the desired order is to sort them. This requires O(|E|log|E|) time using a comparison sorting algorithmSorting algorithm
In computer science, a sorting algorithm is an algorithm that puts elements of a list in a certain order. The most-used orders are numerical order and lexicographical order...
. We also need to test for each x whether A U {x} is independent; assuming independence tests require O(f(|E|)) time, the total time for the algorithm is O(|E|log|E| + |E|f(|E|)).
If we want to find a minimum spanning tree instead, we simply "invert" the weight function by subtracting it from a large constant. More specifically, let wmin(x) = W - w(x), where W exceeds the total weight over all graph edges. Many more optimization problems about all sorts of matroids and weight functions can be solved in this trivial way, although in many cases more efficient algorithms can be found that exploit more specialized properties.
Matroid requirement
Note also that if we take a set of "independent" sets which is a down-set but not a matroid, then the greedy algorithm will not always work. For then there are independent sets
of "independent" sets which is a down-set but not a matroid, then the greedy algorithm will not always work. For then there are independent sets 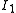 and
and 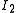 with
with  , but such that for no
, but such that for no 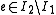 is
is 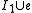 independent.
independent.Pick an
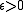 and
and  such that
such that  . Weight the elements of
. Weight the elements of  in the range
in the range 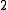 to
to 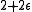 , the elements of
, the elements of 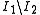 in the range
in the range  to
to  , the elements of
, the elements of 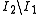 in the range
in the range 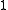 to
to 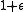 , and the rest in the range
, and the rest in the range 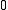 to
to  . The greedy algorithm will select the elements of
. The greedy algorithm will select the elements of 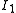 , and then cannot pick any elements of
, and then cannot pick any elements of  . Therefore the independent set it constructs will be of weight at most
. Therefore the independent set it constructs will be of weight at most  , which is smaller than the weight of
, which is smaller than the weight of  .
.History
It was not until 1971 that Jack EdmondsJack Edmonds
Jack R. Edmonds is a mathematician, regarded as one of the most important contributors to the field of combinatorial optimization...
connected weighted matroids to greedy algorithms in his paper "Matroids and the greedy algorithm". Korte and Lovász would generalize these ideas to objects called greedoid
Greedoid
In combinatorics, a greedoid is a type of set system. It arises from the notion of the matroid, which was originally introduced by Whitney in 1935 to study planar graphs and was later used by Edmonds to characterize a class of optimization problems that can be solved by greedy algorithms...
s, which allow even larger classes of problems to be solved by greedy algorithms.

