
Weibull modulus
Encyclopedia
The Weibull modulus is a dimensionless parameter
of the Weibull distribution which is used to describe variability in measured material strength
of brittle materials. For ceramics and other brittle materials, the maximum stress
that a sample can be measured to withstand before failure may vary from specimen to specimen, even under identical testing conditions. This is related to the distribution of physical flaws present in the surface or body of the brittle specimen since brittle failure processes originate at these weak points. When flaws are consistent and evenly distributed, samples will behave more uniformly than when flaws are clustered inconsistently. This must be taken into account when describing the strength of the material, so strength is best represented as a distribution of values rather than as one specific value. The Weibull modulus is a shape parameter for the Weibull distribution model which, in this case, maps the probability of failure of a component at varying stresses.
Consider strength measurements made on many small samples of a brittle ceramic material. If the measurements show little variation
from sample to sample, the calculated Weibull modulus will be high and a single strength value would serve as a good description of the sample-to-sample performance. It may be concluded that its physical flaws, whether inherent to the material itself or resulting from the manufacturing process, are distributed uniformly throughout the material. If the measurements show high variation, the calculated Weibull modulus will be low; this reveals that flaws are clustered inconsistently and the measured strength will be generally weak and variable. Products made from components of low Weibull modulus will exhibit low reliability and their strengths will be broadly distributed.
Test procedures for determining the Weibull modulus are specified in DIN EN 843-5 and DIN 51 110-3.
A further method to determine the strength of brittle materials has been described by the Wikibook contribution "Strength of materials/Weakest link determination by use of three parameter Weibull statistics"http://en.wikibooks.org/wiki/Strength_of_materials/Weakest_link_determination_by_use_of_three_parameter_Weibull_statistics.
of the strength, X, is a Weibull distribution with its density
given by
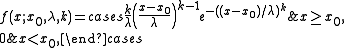
then k is the Weibull modulus.
Dimensionless quantity
In dimensional analysis, a dimensionless quantity or quantity of dimension one is a quantity without an associated physical dimension. It is thus a "pure" number, and as such always has a dimension of 1. Dimensionless quantities are widely used in mathematics, physics, engineering, economics, and...
of the Weibull distribution which is used to describe variability in measured material strength
Strength of materials
In materials science, the strength of a material is its ability to withstand an applied stress without failure. The applied stress may be tensile, compressive, or shear. Strength of materials is a subject which deals with loads, deformations and the forces acting on a material. A load applied to a...
of brittle materials. For ceramics and other brittle materials, the maximum stress
Stress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
that a sample can be measured to withstand before failure may vary from specimen to specimen, even under identical testing conditions. This is related to the distribution of physical flaws present in the surface or body of the brittle specimen since brittle failure processes originate at these weak points. When flaws are consistent and evenly distributed, samples will behave more uniformly than when flaws are clustered inconsistently. This must be taken into account when describing the strength of the material, so strength is best represented as a distribution of values rather than as one specific value. The Weibull modulus is a shape parameter for the Weibull distribution model which, in this case, maps the probability of failure of a component at varying stresses.
Consider strength measurements made on many small samples of a brittle ceramic material. If the measurements show little variation
Statistical dispersion
In statistics, statistical dispersion is variability or spread in a variable or a probability distribution...
from sample to sample, the calculated Weibull modulus will be high and a single strength value would serve as a good description of the sample-to-sample performance. It may be concluded that its physical flaws, whether inherent to the material itself or resulting from the manufacturing process, are distributed uniformly throughout the material. If the measurements show high variation, the calculated Weibull modulus will be low; this reveals that flaws are clustered inconsistently and the measured strength will be generally weak and variable. Products made from components of low Weibull modulus will exhibit low reliability and their strengths will be broadly distributed.
Test procedures for determining the Weibull modulus are specified in DIN EN 843-5 and DIN 51 110-3.
A further method to determine the strength of brittle materials has been described by the Wikibook contribution "Strength of materials/Weakest link determination by use of three parameter Weibull statistics"http://en.wikibooks.org/wiki/Strength_of_materials/Weakest_link_determination_by_use_of_three_parameter_Weibull_statistics.
Definition
If the probability distributionProbability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of the strength, X, is a Weibull distribution with its density
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
given by
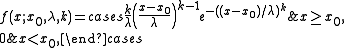
then k is the Weibull modulus.
External links
- Weibull modulus at Breviary Technical Ceramics

