Wedderburn's little theorem
Encyclopedia
In mathematics, Wedderburn's little theorem states that every finite domain
is a field
. In other words, for finite ring
s, there is no distinction between domains, skew-fields and fields.
The Artin–Zorn theorem generalizes the theorem to alternative rings.
in 1905, who went on to prove it two other ways. Another proof was given by Leonard Eugene Dickson
shortly after Wedderburn's original proof, and Dickson acknowledged Wedderburn's priority. However, as noted in , Wedderburn's first proof was incorrect – it had a gap – and his subsequent proofs came after he had read Dickson's correct proof. On this basis, Parshall argues that Dickson should be credited with the first correct proof.
A simplified version of the proof was later given by Ernst Witt
. Witt's proof is sketched below. Alternatively, the theorem is a consequence of the Skolem–Noether theorem
.
be a finite domain. For each nonzero 
, the map
is injective; thus, surjective. Hence,
has a left inverse. By the same argument, 
has a right inverse. A is thus a skew-field
. Since the center
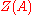of 
is a field, 
is a vector space over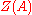 
with finite dimension n. Our objective is then to show 
. If 
is the order of 
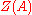, then A has order 
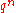. For each 
that is not in the center, the centralizer
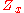of x has order 
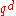where d divides n. Viewing 
, 
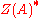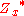and 
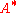as groups under multiplication, we can write the class equation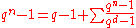
where the sum is taken over all representatives
that is not in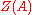 
and d are the numbers discussed above. 
and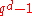 
both admit factorization in terms of cyclotomic polynomials 
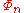. After cancellation, we see that 
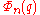divides 
and 
, so it must divide 
. So we reach contradiction unless 
.
Domain (ring theory)
In mathematics, especially in the area of abstract algebra known as ring theory, a domain is a ring such that ab = 0 implies that either a = 0 or b = 0. That is, it is a ring which has no left or right zero divisors. Some authors require the ring to be nontrivial...
is a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
. In other words, for finite ring
Finite ring
In mathematics, more specifically abstract algebra, a finite ring is a ring that has a finite number of elements....
s, there is no distinction between domains, skew-fields and fields.
The Artin–Zorn theorem generalizes the theorem to alternative rings.
History
The original proof was given by Joseph WedderburnJoseph Wedderburn
Joseph Henry Maclagan Wedderburn was a Scottish mathematician, who taught at Princeton University for most of his career. A significant algebraist, he proved that a finite division algebra is a field, and part of the Artin–Wedderburn theorem on simple algebras...
in 1905, who went on to prove it two other ways. Another proof was given by Leonard Eugene Dickson
Leonard Eugene Dickson
Leonard Eugene Dickson was an American mathematician. He was one of the first American researchers in abstract algebra, in particular the theory of finite fields and classical groups, and is also remembered for a three-volume history of number theory.-Life:Dickson considered himself a Texan by...
shortly after Wedderburn's original proof, and Dickson acknowledged Wedderburn's priority. However, as noted in , Wedderburn's first proof was incorrect – it had a gap – and his subsequent proofs came after he had read Dickson's correct proof. On this basis, Parshall argues that Dickson should be credited with the first correct proof.
A simplified version of the proof was later given by Ernst Witt
Ernst Witt
Ernst Witt was a German mathematician born on the island of Als . Shortly after his birth, he and his parents moved to China, and he did not return to Europe until he was nine....
. Witt's proof is sketched below. Alternatively, the theorem is a consequence of the Skolem–Noether theorem
Skolem–Noether theorem
In mathematics, the Skolem–Noether theorem, named after Thoralf Skolem and Emmy Noether, is an important result in ring theory which characterizes the automorphisms of simple rings....
.
Sketch of proof
Let be a finite domain. For each nonzero , the mapis injective; thus, surjective. Hence,
has a left inverse. By the same argument, has a right inverse. A is thus a skew-fieldDivision ring
In abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...
. Since the center
Center (group theory)
In abstract algebra, the center of a group G, denoted Z,The notation Z is from German Zentrum, meaning "center". is the set of elements that commute with every element of G. In set-builder notation,...
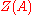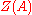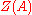of is a field, is a vector space over with finite dimension n. Our objective is then to show . If is the order of , then A has order 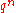. For each that is not in the center, the centralizerCentralizer and normalizer
In group theory, the centralizer and normalizer of a subset S of a group G are subgroups of G which have a restricted action on the elements of S and S as a whole, respectively...
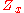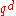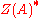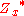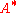of x has order where d divides n. Viewing , and as groups under multiplication, we can write the class equation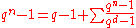where the sum is taken over all representatives
that is not in 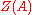and d are the numbers discussed above. and 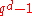both admit factorization in terms of cyclotomic polynomials 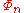. After cancellation, we see that 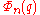divides and , so it must divide . So we reach contradiction unless .