War of attrition (game)
Encyclopedia
In game theory
, the war of attrition is a model of aggression in which two contestants compete
for a resource of value V by persisting while constantly accumulating costs over the time t that the contest lasts. The model was originally formulated by John Maynard Smith
, a mixed evolutionary stable strategy (ESS) was determined by Bishop & Cannings. Strategically, the game is an auction
, in which the prize goes to the player with the highest bid, and each player pays the loser's low bid (making it an all-pay
sealed-bid second-price auction).
The game works as follows: Each player makes a bid; the one who bids the highest wins a resource of value V. Each player pays the lowest bid, a.
The premise that the players may bid any number is important to analysis of the game. The bid may even exceed the value of the resource that is contested over. This at first appears to be irrational, being seemingly foolish to pay more for a resource than its value; however, remember that each bidder only pays the low bid. Therefore, it would seem to be in each player's best interest to bid the maximum possible amount rather than an amount equal to or less than the value of the resource.
There is a catch, however; if both players bid higher than V, the high bidder does not so much win as lose less. This situation is commonly referred to as a Pyrrhic victory
. In contrast, if each player bids less than V, the player bidding a will lose, and the other player will benefit by an amount of V-a. If each player bids the same amount for a less than V/2, they split the value of V, each gaining V/2-a. For a tie such that a>V/2, they both lose the difference of V/2 and a. Luce
and Raiffa
referred to the latter situation as a "ruinous situation"; the point at which both players suffer, and there is no winner.
The conclusion one can draw from this pseudo-matrix is that there is no value to bid which is beneficial in all cases, so there is no dominant strategy. However, this fact and the above argument do not preclude the existence of Nash Equilibria. Any pair of strategies with the following characteristics is a Nash Equilibrium
:
With these strategies, one player wins and pays zero, and the other player loses and pays zero. It is easy to verify that neither player can strictly gain by unilaterally deviating.
. Time is modeled as a continuous variable which starts at zero and runs indefinitely. Each player chooses when to concede the object to the other player. In the case of a tie, each player receives 
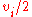utility. Time is valuable, each player uses one unit of utility per period of time. This formulation is slightly more complex since it allows each player to assign a different value to the object. Its equilibria are not as obvious as the other formulation.The evolutionary stable strategy is a mixed ESS, in which the probability of persisting for a length of time t is:
The evolutionary stable strategy below represents the most probable value of a. The value p(t) for a contest with a resource of value V over time t, is the probability that t = a. This strategy does not guarantee the win; rather it is the optimal balance of risk and reward. The outcome of any particular game cannot be predicted as the random factor of the opponent's bid is too unpredictable.
That no pure persistence time is an ESS can be demonstrated simply by considering a putative ESS bid of x, which will be beaten by a bid of x+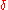
.
when playing this game is a probability density of random persistence times which cannot be predicted by the opponent in any particular contest. This result has led to the prediction that threat displays ought not to evolve, and to the conclusion in The Illuminatus! Trilogy
that optimal military strategy is to behave in a completely unpredictable, and therefore insane, manner. Neither of these conclusions appear to be truly quantifiably reasonable applications of the model to realistic conditions.
.
Game theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
, the war of attrition is a model of aggression in which two contestants compete
Competition
Competition is a contest between individuals, groups, animals, etc. for territory, a niche, or a location of resources. It arises whenever two and only two strive for a goal which cannot be shared. Competition occurs naturally between living organisms which co-exist in the same environment. For...
for a resource of value V by persisting while constantly accumulating costs over the time t that the contest lasts. The model was originally formulated by John Maynard Smith
John Maynard Smith
John Maynard Smith,His surname was Maynard Smith, not Smith, nor was it hyphenated. F.R.S. was a British theoretical evolutionary biologist and geneticist. Originally an aeronautical engineer during the Second World War, he took a second degree in genetics under the well-known biologist J.B.S....
, a mixed evolutionary stable strategy (ESS) was determined by Bishop & Cannings. Strategically, the game is an auction
Auction
An auction is a process of buying and selling goods or services by offering them up for bid, taking bids, and then selling the item to the highest bidder...
, in which the prize goes to the player with the highest bid, and each player pays the loser's low bid (making it an all-pay
All-pay auction
In economics and game theory an all-pay auction, is an auction in which all bidders must pay regardless of whether they win the prize, which is awarded to the highest bidder as in a conventional auction...
sealed-bid second-price auction).
Examining the game
The war of attrition cannot be properly solved using the payoff matrix. The players' available resources are the only limit to the maximum value of bids; bids can be any number if available resources are ignored, meaning that for any value of α, there is a value β that is greater. Attempting to put all possible bids onto the matrix, however, will result in an ∞×∞ matrix. One can, however, use a pseudo-matrix form of war of attrition to understand the basic workings of the game, and analyze some of the problems in representing the game in this manner.The game works as follows: Each player makes a bid; the one who bids the highest wins a resource of value V. Each player pays the lowest bid, a.
The premise that the players may bid any number is important to analysis of the game. The bid may even exceed the value of the resource that is contested over. This at first appears to be irrational, being seemingly foolish to pay more for a resource than its value; however, remember that each bidder only pays the low bid. Therefore, it would seem to be in each player's best interest to bid the maximum possible amount rather than an amount equal to or less than the value of the resource.
There is a catch, however; if both players bid higher than V, the high bidder does not so much win as lose less. This situation is commonly referred to as a Pyrrhic victory
Pyrrhic victory
A Pyrrhic victory is a victory with such a devastating cost to the victor that it carries the implication that another such victory will ultimately cause defeat.-Origin:...
. In contrast, if each player bids less than V, the player bidding a will lose, and the other player will benefit by an amount of V-a. If each player bids the same amount for a less than V/2, they split the value of V, each gaining V/2-a. For a tie such that a>V/2, they both lose the difference of V/2 and a. Luce
R. Duncan Luce
Robert Duncan Luce is the Distinguished Research Professor of Cognitive Science at the University of California, Irvine.Luce received a B.S. in Aeronautical Engineering from the Massachusetts Institute of Technology in 1945, and PhD in Mathematics from the same university in 1950...
and Raiffa
Howard Raiffa
Howard Raiffa is the Frank P. Ramsey Professor of Managerial Economics, a joint chair held by the Business School and the Kennedy School of Government at Harvard University...
referred to the latter situation as a "ruinous situation"; the point at which both players suffer, and there is no winner.
The conclusion one can draw from this pseudo-matrix is that there is no value to bid which is beneficial in all cases, so there is no dominant strategy. However, this fact and the above argument do not preclude the existence of Nash Equilibria. Any pair of strategies with the following characteristics is a Nash Equilibrium
Nash equilibrium
In game theory, Nash equilibrium is a solution concept of a game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only his own strategy unilaterally...
:
- One player bids zero
- The other player bids any value equal to V or higher, or mixes among any values V or higher.
With these strategies, one player wins and pays zero, and the other player loses and pays zero. It is easy to verify that neither player can strictly gain by unilaterally deviating.
Dynamic formulation and Evolutionary stable strategy
Another popular formulation of the war of attrition is as follows: Two players are involved in a dispute. The value of the object to each player is. Time is modeled as a continuous variable which starts at zero and runs indefinitely. Each player chooses when to concede the object to the other player. In the case of a tie, each player receives 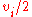utility. Time is valuable, each player uses one unit of utility per period of time. This formulation is slightly more complex since it allows each player to assign a different value to the object. Its equilibria are not as obvious as the other formulation.The evolutionary stable strategy is a mixed ESS, in which the probability of persisting for a length of time t is:The evolutionary stable strategy below represents the most probable value of a. The value p(t) for a contest with a resource of value V over time t, is the probability that t = a. This strategy does not guarantee the win; rather it is the optimal balance of risk and reward. The outcome of any particular game cannot be predicted as the random factor of the opponent's bid is too unpredictable.
That no pure persistence time is an ESS can be demonstrated simply by considering a putative ESS bid of x, which will be beaten by a bid of x+
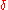.The ESS in popular culture
The evolutionarily stable strategyEvolutionarily stable strategy
In game theory and behavioural ecology, an evolutionarily stable strategy , which is sometimes also called an evolutionary stable strategy, is a strategy which, if adopted by a population of players, cannot be invaded by any alternative strategy that is initially rare. An ESS is an equilibrium...
when playing this game is a probability density of random persistence times which cannot be predicted by the opponent in any particular contest. This result has led to the prediction that threat displays ought not to evolve, and to the conclusion in The Illuminatus! Trilogy
The Illuminatus! Trilogy
The Illuminatus! Trilogy is a series of three novels written by Robert Shea and Robert Anton Wilson first published in 1975. The trilogy is a satirical, postmodern, science fiction-influenced adventure story; a drug-, sex-, and magick-laden trek through a number of conspiracy theories, both...
that optimal military strategy is to behave in a completely unpredictable, and therefore insane, manner. Neither of these conclusions appear to be truly quantifiably reasonable applications of the model to realistic conditions.
Conclusions
By examining the unusual results of this game, it serves to mathematically prove another piece of old wisdom: "Expect the unexpected". By making the assumption that an opponent will act irrationally, one can paradoxically better predict their actions, as they are limited in this game. They will either act rationally, and take the optimal decision, or they will be irrational, and take the non-optimal solution. If one considers the irrational as a bluff and the rational as backing down from a bluff, it transforms the game into another game theory game, Hawk and DoveChicken (game)
The game of chicken, also known as the hawk-dove or snowdrift game, is an influential model of conflict for two players in game theory...
.
See also
- Bishop-Cannings theoremBishop-Cannings theoremThe Bishop–Cannings theorem is a theorem in evolutionary game theory. It states that all members of a mixed evolutionarily stable strategy have the same payoff , and that none of these can also be a pure ESS...
- Hawk-dove game
- Dollar auctionDollar auctionThe dollar auction is a non-zero sum sequential game designed by economist Martin Shubik to illustrate a paradox brought about by traditional rational choice theory in which players with perfect information in the game are compelled to make an ultimately irrational decision based completely on a...
- Attrition warfareAttrition warfareAttrition warfare is a military strategy in which a belligerent side attempts to win a war by wearing down its enemy to the point of collapse through continuous losses in personnel and matériel....
Sources
- Bishop, D.T., Cannings, C. & Maynard Smith, J.John Maynard SmithJohn Maynard Smith,His surname was Maynard Smith, not Smith, nor was it hyphenated. F.R.S. was a British theoretical evolutionary biologist and geneticist. Originally an aeronautical engineer during the Second World War, he took a second degree in genetics under the well-known biologist J.B.S....
(1978) The war of attrition with random rewards. Journal of Theoretical Biology 74:377-389. - Maynard Smith, J.John Maynard SmithJohn Maynard Smith,His surname was Maynard Smith, not Smith, nor was it hyphenated. F.R.S. was a British theoretical evolutionary biologist and geneticist. Originally an aeronautical engineer during the Second World War, he took a second degree in genetics under the well-known biologist J.B.S....
& Parker, G. A.Geoff ParkerProfessor Geoffrey Alan Parker FRS is a Derby professor of biology at the University of Liverpool.He has a particular interest in behavioural ecology and evolutionary biology, and is most noted for introducing the concept of sperm competition in 1970.Much of his work from the 1970s onwards has...
(1976). The logic of asymmetric contests. Animal Behaviour. 24:159-175. - Luce,R.D.R. Duncan LuceRobert Duncan Luce is the Distinguished Research Professor of Cognitive Science at the University of California, Irvine.Luce received a B.S. in Aeronautical Engineering from the Massachusetts Institute of Technology in 1945, and PhD in Mathematics from the same university in 1950...
& Raiffa, H.Howard RaiffaHoward Raiffa is the Frank P. Ramsey Professor of Managerial Economics, a joint chair held by the Business School and the Kennedy School of Government at Harvard University...
(1957) "Games and Decisions: Introduction and Critical Survey"(originally published as "A Study of the Behavioral Models Project, Bureau of Applied Social Research") John Wiley & Sons Inc., New York - Rapaport,AnatolAnatol RapoportAnatol Rapoport was a Russian-born American Jewish mathematical psychologist. He contributed to general systems theory, mathematical biology and to the mathematical modeling of social interaction and stochastic models of contagion.-Biography:...
(1966) "Two Person Game Theory" University of Michigan Press, Ann Arbor
External links
- Exposition of the derivation of the ESS - From Ken Prestwich's Game Theory website at College of the Holy Cross