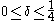Walsh code
Encyclopedia
In coding theory
, the Walsh–Hadamard code, named after the American mathematician Joseph Leonard Walsh
and the French mathematician Jacques Hadamard
, is an example of a linear code
over a binary alphabet that maps messages of length to codewords of length
to codewords of length 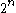 . The Walsh–Hadamard code is unique in that each non-zero codeword has Hamming weight
. The Walsh–Hadamard code is unique in that each non-zero codeword has Hamming weight
of exactly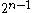 , which implies that the distance
, which implies that the distance
of the code is also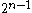 . In standard coding theory
. In standard coding theory
notation, this means that the Walsh–Hadamard code is a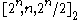 -code. The Hadamard code
-code. The Hadamard code
can be seen as a slightly improved version of the Walsh–Hadamard code as it achieves the same block length and minimum distance with a message length of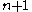 , that is, it can transmit one more bit of information per codeword, but this improvement comes at the expense of a slightly more complicated construction.
, that is, it can transmit one more bit of information per codeword, but this improvement comes at the expense of a slightly more complicated construction.
The Walsh–Hadamard code is a locally decodable
code, which provides a way to recover parts of the original message with high probability, while only looking at a small fraction of the received word. This gives rise to applications in computational complexity theory
and particularly in the design of probabilistically checkable proofs. It can also be shown that, using list decoding, the original message can be recovered as long as less than 1/2 of the bits in the received word have been corrupted.
In code division multiple access
(CDMA) communication, the Walsh–Hadamard code is used to define individual communication channels
. It is usual in the CDMA literature to refer to codewords as “codes”. Each user will use a different codeword, or “code”, to modulate their signal. Because Walsh–Hadamard codewords are mathematically orthogonal, a Walsh-encoded signal appears as random noise to a CDMA capable mobile terminal
, unless that terminal uses the same codeword as the one used to encode the incoming signal.
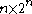 generator matrix
generator matrix
 for the Walsh–Hadamard code of dimension
for the Walsh–Hadamard code of dimension
 is given by
is given by

where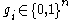 is the vector corresponding to the binary representation of
is the vector corresponding to the binary representation of 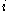 . In other words,
. In other words, 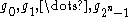 is the list of all vectors of
is the list of all vectors of 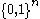 in some lexicographic order. For example, the generator matrix
in some lexicographic order. For example, the generator matrix
for the Walsh–Hadamard code of dimension 3 is
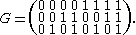
As is possible for any linear code generated by a generator matrix, we encode a message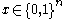 , viewed as a row vector, by computing its codeword
, viewed as a row vector, by computing its codeword 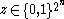 using the vector-matrix product in the vector space
using the vector-matrix product in the vector space
over the finite field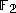 :
: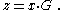
This way, the matrix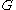 defines a linear operator
defines a linear operator 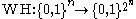 and we can write
and we can write 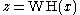 .
.
A more explicit, equivalent definition of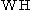 uses the scalar product
uses the scalar product 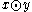 over
over 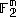 :
:
Then the Walsh–Hadamard code is the function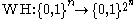 that maps every string
that maps every string 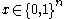 into the string
into the string 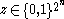 satisfying
satisfying 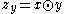 for every
for every 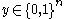 (where
(where 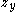 denotes the
denotes the 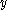 th coordinate of
th coordinate of  , identifying
, identifying 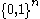 with
with  in some way).
in some way).
between any two distinct codewords, i.e., the minimum number of positions at which two distinct codewords differ.
Since the Walsh–Hadamard code is a linear code
, the distance is equal to the minimum Hamming weight
among all of its non-zero codewords. All non-zero codewords of the Walsh–Hadamard code have a Hamming weight
of exactly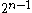 by the following argument.
by the following argument.
Let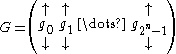 be the
be the 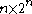 generator matrix
generator matrix
for a Walsh-Hadamard code of dimension
 .
.
Let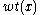 represent the Hamming weight
represent the Hamming weight
of vector .
.
Let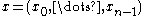 be a non-zero message in
be a non-zero message in 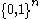 .
.
We want to show that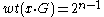 for all non-zero codewords. Remember that all arithmetic is done over
for all non-zero codewords. Remember that all arithmetic is done over 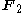 , which is the finite field
, which is the finite field
of size 2.
Let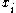 be a non-zero bit of arbitrary message,
be a non-zero bit of arbitrary message,  . Pair up the columns of
. Pair up the columns of 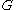 such that for each pair
such that for each pair 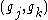 ,
, 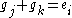 (where
(where 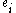 is the zero vector with a 1 in the
is the zero vector with a 1 in the 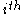 position). By the way
position). By the way 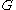 is constructed, there will be exactly
is constructed, there will be exactly 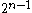 pairs. Then note that
pairs. Then note that 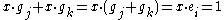 .
. 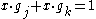 , implies that exactly one of
, implies that exactly one of 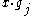 ,
, 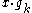 must be 1. There are
must be 1. There are 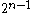 pairs, so
pairs, so 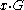 will have exactly
will have exactly 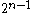 bits that are a 1.
bits that are a 1.
Therefore, the Hamming weight
of every codeword in the code is exactly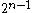 .
.
Being a linear code, this means that the distance of the Walsh-Hadamard code is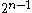 .
.
code is a code that allows a single bit of the original message to be recovered with high probability by only looking at a small portion of the received word. A code is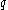 -query locally decodable
-query locally decodable
if a message bit,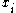 , can be recovered by checking
, can be recovered by checking 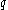 bits of the received word. More formally, a code,
bits of the received word. More formally, a code, 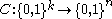 , is
, is 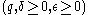 -locally decodable, if there exists a probabilistic decoder,
-locally decodable, if there exists a probabilistic decoder, 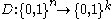 , such that (Note:
, such that (Note: 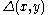 represents the Hamming distance
represents the Hamming distance
between vectors and
and 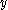 ):
):
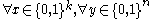 ,
, 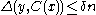 implies that
implies that 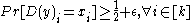
Theorem 1: The Walsh–Hadamard code is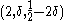 -locally decodable for
-locally decodable for 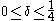 .
.
Lemma 1: For all codewords, in a Walsh–Hadamard code,
in a Walsh–Hadamard code, 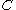 ,
, 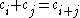 , where
, where 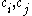 represent the bits in
represent the bits in  in positions
in positions 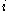 and
and 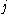 respectively, and
respectively, and 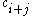 represents the bit at position
represents the bit at position 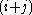 .
.
Let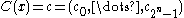 be the codeword in
be the codeword in 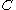 corresponding to message
corresponding to message 
Let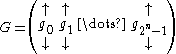 be the generator matrix of
be the generator matrix of 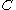
By definition,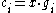 . From this,
. From this, 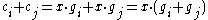 . By the construction of
. By the construction of 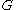 ,
, 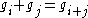 . Therefore, by substitution,
. Therefore, by substitution, 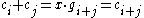 .
.
To prove theorem 1 we will construct a decoding algorithm and prove its correctness.
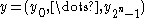
For each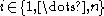 :
:
Output: Message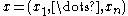
 , and received word
, and received word 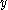 such that
such that 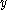 differs from
differs from 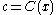 on at most
on at most 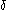 fraction of bits,
fraction of bits, 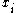 can be decoded with probability at least
can be decoded with probability at least 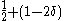 .
.
By lemma 1,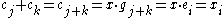 . Since
. Since 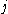 and
and 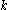 are picked uniformly, the probability that
are picked uniformly, the probability that 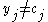 is at most
is at most 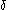 . Similarly, the probability that
. Similarly, the probability that 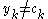 is at most
is at most 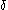 . By the union bound, the probability that either
. By the union bound, the probability that either 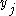 or
or 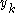 do not match the corresponding bits in
do not match the corresponding bits in  is at most
is at most 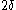 . If both
. If both 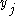 and
and 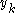 correspond to
correspond to  , then lemma 1 will apply, and therefore, the proper value of
, then lemma 1 will apply, and therefore, the proper value of 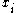 will be computed. Therefore the probability
will be computed. Therefore the probability 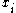 is decoded properly is at least
is decoded properly is at least 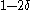 . Therefore,
. Therefore, 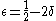 and for
and for  to be positive,
to be positive, 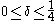 .
.
Therefore, the Walsh–Hadamard code is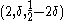 locally decodable for
locally decodable for 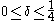
Coding theory
Coding theory is the study of the properties of codes and their fitness for a specific application. Codes are used for data compression, cryptography, error-correction and more recently also for network coding...
, the Walsh–Hadamard code, named after the American mathematician Joseph Leonard Walsh
Joseph Leonard Walsh
Joseph Leonard Walsh, was an American mathematician. His work was mainly in the field of analysis.For most of his professional career he studied and worked at Harvard University. He received a B.S. in 1916 and a PhD in 1920. The Advisor of his PhD was Maxime Bôcher...
and the French mathematician Jacques Hadamard
Jacques Hadamard
Jacques Salomon Hadamard FRS was a French mathematician who made major contributions in number theory, complex function theory, differential geometry and partial differential equations.-Biography:...
, is an example of a linear code
Linear code
In coding theory, a linear code is an error-correcting code for which any linear combination of codewords is also a codeword. Linear codes are traditionally partitioned into block codes and convolutional codes, although Turbo codes can be seen as a hybrid of these two types. Linear codes allow for...
over a binary alphabet that maps messages of length
 to codewords of length
to codewords of length 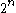 . The Walsh–Hadamard code is unique in that each non-zero codeword has Hamming weight
. The Walsh–Hadamard code is unique in that each non-zero codeword has Hamming weightHamming weight
The Hamming weight of a string is the number of symbols that are different from the zero-symbol of the alphabet used. It is thus equivalent to the Hamming distance from the all-zero string of the same length. For the most typical case, a string of bits, this is the number of 1's in the string...
of exactly
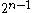 , which implies that the distance
, which implies that the distanceHamming distance
In information theory, the Hamming distance between two strings of equal length is the number of positions at which the corresponding symbols are different...
of the code is also
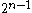 . In standard coding theory
. In standard coding theoryCoding theory
Coding theory is the study of the properties of codes and their fitness for a specific application. Codes are used for data compression, cryptography, error-correction and more recently also for network coding...
notation, this means that the Walsh–Hadamard code is a
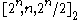 -code. The Hadamard code
-code. The Hadamard codeHadamard code
The Hadamard code is an error-correcting code that is used for error detection and correction when transmitting messages over very noisy or unreliable channels....
can be seen as a slightly improved version of the Walsh–Hadamard code as it achieves the same block length and minimum distance with a message length of
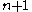 , that is, it can transmit one more bit of information per codeword, but this improvement comes at the expense of a slightly more complicated construction.
, that is, it can transmit one more bit of information per codeword, but this improvement comes at the expense of a slightly more complicated construction.The Walsh–Hadamard code is a locally decodable
Locally decodable
A locally decodable code is an error-correcting code that allows to decode a single bit of a message with high probability by only looking at a small number of bits of a possibly partially corrupted codeword....
code, which provides a way to recover parts of the original message with high probability, while only looking at a small fraction of the received word. This gives rise to applications in computational complexity theory
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
and particularly in the design of probabilistically checkable proofs. It can also be shown that, using list decoding, the original message can be recovered as long as less than 1/2 of the bits in the received word have been corrupted.
In code division multiple access
Code division multiple access
Code division multiple access is a channel access method used by various radio communication technologies. It should not be confused with the mobile phone standards called cdmaOne, CDMA2000 and WCDMA , which are often referred to as simply CDMA, and use CDMA as an underlying channel access...
(CDMA) communication, the Walsh–Hadamard code is used to define individual communication channels
Channel (communications)
In telecommunications and computer networking, a communication channel, or channel, refers either to a physical transmission medium such as a wire, or to a logical connection over a multiplexed medium such as a radio channel...
. It is usual in the CDMA literature to refer to codewords as “codes”. Each user will use a different codeword, or “code”, to modulate their signal. Because Walsh–Hadamard codewords are mathematically orthogonal, a Walsh-encoded signal appears as random noise to a CDMA capable mobile terminal
Terminal (telecommunication)
In the context of telecommunications, a terminal is a device which is capable of communicating over a line. Examples of terminals are telephones, fax machines, and network devices - printers and workstations....
, unless that terminal uses the same codeword as the one used to encode the incoming signal.
Definition
The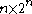 generator matrix
generator matrixGenerator matrix
In coding theory, a generator matrix is a basis for a linear code, generating all its possible codewords.If the matrix is G and the linear code is C,where w is a codeword of the linear code C, c is a row vector, and a bijection exists between w and c. A generator matrix for an q-code has...
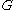 for the Walsh–Hadamard code of dimension
for the Walsh–Hadamard code of dimensionDimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
 is given by
is given by
where
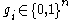 is the vector corresponding to the binary representation of
is the vector corresponding to the binary representation of 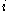 . In other words,
. In other words, 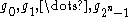 is the list of all vectors of
is the list of all vectors of 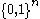 in some lexicographic order. For example, the generator matrix
in some lexicographic order. For example, the generator matrixGenerator matrix
In coding theory, a generator matrix is a basis for a linear code, generating all its possible codewords.If the matrix is G and the linear code is C,where w is a codeword of the linear code C, c is a row vector, and a bijection exists between w and c. A generator matrix for an q-code has...
for the Walsh–Hadamard code of dimension 3 is
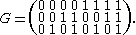
As is possible for any linear code generated by a generator matrix, we encode a message
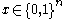 , viewed as a row vector, by computing its codeword
, viewed as a row vector, by computing its codeword 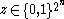 using the vector-matrix product in the vector space
using the vector-matrix product in the vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over the finite field
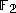 :
: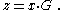
This way, the matrix
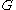 defines a linear operator
defines a linear operator 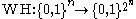 and we can write
and we can write 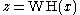 .
.A more explicit, equivalent definition of
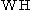 uses the scalar product
uses the scalar product 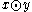 over
over 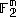 :
:- For any two strings
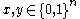 , we have
, we have 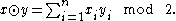
Then the Walsh–Hadamard code is the function
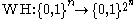 that maps every string
that maps every string 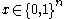 into the string
into the string 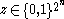 satisfying
satisfying 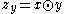 for every
for every 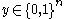 (where
(where 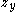 denotes the
denotes the 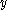 th coordinate of
th coordinate of  , identifying
, identifying 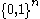 with
with  in some way).
in some way).Distance
The distance of a code is the minimum Hamming distanceHamming distance
In information theory, the Hamming distance between two strings of equal length is the number of positions at which the corresponding symbols are different...
between any two distinct codewords, i.e., the minimum number of positions at which two distinct codewords differ.
Since the Walsh–Hadamard code is a linear code
Linear code
In coding theory, a linear code is an error-correcting code for which any linear combination of codewords is also a codeword. Linear codes are traditionally partitioned into block codes and convolutional codes, although Turbo codes can be seen as a hybrid of these two types. Linear codes allow for...
, the distance is equal to the minimum Hamming weight
Hamming weight
The Hamming weight of a string is the number of symbols that are different from the zero-symbol of the alphabet used. It is thus equivalent to the Hamming distance from the all-zero string of the same length. For the most typical case, a string of bits, this is the number of 1's in the string...
among all of its non-zero codewords. All non-zero codewords of the Walsh–Hadamard code have a Hamming weight
Hamming weight
The Hamming weight of a string is the number of symbols that are different from the zero-symbol of the alphabet used. It is thus equivalent to the Hamming distance from the all-zero string of the same length. For the most typical case, a string of bits, this is the number of 1's in the string...
of exactly
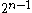 by the following argument.
by the following argument.Let
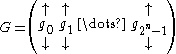 be the
be the 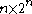 generator matrix
generator matrixGenerator matrix
In coding theory, a generator matrix is a basis for a linear code, generating all its possible codewords.If the matrix is G and the linear code is C,where w is a codeword of the linear code C, c is a row vector, and a bijection exists between w and c. A generator matrix for an q-code has...
for a Walsh-Hadamard code of dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
 .
.Let
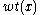 represent the Hamming weight
represent the Hamming weightHamming weight
The Hamming weight of a string is the number of symbols that are different from the zero-symbol of the alphabet used. It is thus equivalent to the Hamming distance from the all-zero string of the same length. For the most typical case, a string of bits, this is the number of 1's in the string...
of vector
 .
.Let
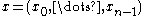 be a non-zero message in
be a non-zero message in 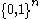 .
.We want to show that
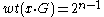 for all non-zero codewords. Remember that all arithmetic is done over
for all non-zero codewords. Remember that all arithmetic is done over 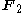 , which is the finite field
, which is the finite fieldFinite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
of size 2.
Let
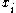 be a non-zero bit of arbitrary message,
be a non-zero bit of arbitrary message,  . Pair up the columns of
. Pair up the columns of 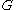 such that for each pair
such that for each pair 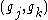 ,
, 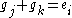 (where
(where 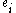 is the zero vector with a 1 in the
is the zero vector with a 1 in the 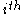 position). By the way
position). By the way 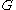 is constructed, there will be exactly
is constructed, there will be exactly 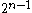 pairs. Then note that
pairs. Then note that 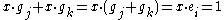 .
. 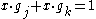 , implies that exactly one of
, implies that exactly one of  ,
, 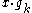 must be 1. There are
must be 1. There are 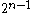 pairs, so
pairs, so 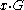 will have exactly
will have exactly 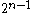 bits that are a 1.
bits that are a 1.Therefore, the Hamming weight
Hamming weight
The Hamming weight of a string is the number of symbols that are different from the zero-symbol of the alphabet used. It is thus equivalent to the Hamming distance from the all-zero string of the same length. For the most typical case, a string of bits, this is the number of 1's in the string...
of every codeword in the code is exactly
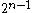 .
.Being a linear code, this means that the distance of the Walsh-Hadamard code is
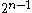 .
.Locally Decodable
A locally decodableLocally decodable
A locally decodable code is an error-correcting code that allows to decode a single bit of a message with high probability by only looking at a small number of bits of a possibly partially corrupted codeword....
code is a code that allows a single bit of the original message to be recovered with high probability by only looking at a small portion of the received word. A code is
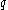 -query locally decodable
-query locally decodableLocally decodable
A locally decodable code is an error-correcting code that allows to decode a single bit of a message with high probability by only looking at a small number of bits of a possibly partially corrupted codeword....
if a message bit,
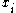 , can be recovered by checking
, can be recovered by checking 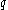 bits of the received word. More formally, a code,
bits of the received word. More formally, a code, 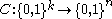 , is
, is 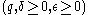 -locally decodable, if there exists a probabilistic decoder,
-locally decodable, if there exists a probabilistic decoder, 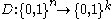 , such that (Note:
, such that (Note: 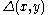 represents the Hamming distance
represents the Hamming distanceHamming distance
In information theory, the Hamming distance between two strings of equal length is the number of positions at which the corresponding symbols are different...
between vectors
 and
and 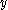 ):
):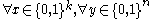 ,
, 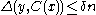 implies that
implies that 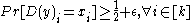
Theorem 1: The Walsh–Hadamard code is
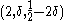 -locally decodable for
-locally decodable for 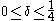 .
.Lemma 1: For all codewords,
 in a Walsh–Hadamard code,
in a Walsh–Hadamard code, 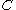 ,
, 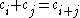 , where
, where 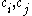 represent the bits in
represent the bits in  in positions
in positions 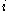 and
and 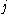 respectively, and
respectively, and 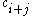 represents the bit at position
represents the bit at position 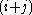 .
.Proof of Lemma 1
----Let
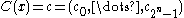 be the codeword in
be the codeword in 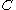 corresponding to message
corresponding to message 
Let
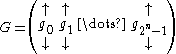 be the generator matrix of
be the generator matrix of 
By definition,
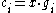 . From this,
. From this, 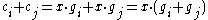 . By the construction of
. By the construction of 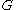 ,
, 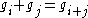 . Therefore, by substitution,
. Therefore, by substitution, 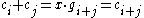 .
.Proof of Theorem 1
----To prove theorem 1 we will construct a decoding algorithm and prove its correctness.
Algorithm
Input: Received word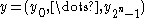
For each
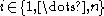 :
:
- Pick
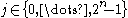 independently at random
independently at random - Pick
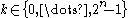 such that
such that 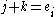 where
where 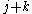 is the bitwise xor of
is the bitwise xor of 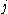 and
and 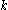 .
. -
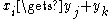
Output: Message
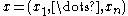
Proof of correctness
For any message, , and received word
, and received word 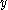 such that
such that 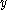 differs from
differs from 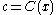 on at most
on at most 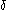 fraction of bits,
fraction of bits, 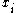 can be decoded with probability at least
can be decoded with probability at least 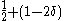 .
.By lemma 1,
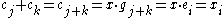 . Since
. Since 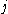 and
and 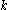 are picked uniformly, the probability that
are picked uniformly, the probability that 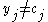 is at most
is at most 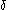 . Similarly, the probability that
. Similarly, the probability that 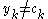 is at most
is at most 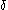 . By the union bound, the probability that either
. By the union bound, the probability that either 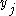 or
or 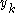 do not match the corresponding bits in
do not match the corresponding bits in  is at most
is at most 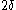 . If both
. If both 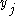 and
and 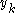 correspond to
correspond to  , then lemma 1 will apply, and therefore, the proper value of
, then lemma 1 will apply, and therefore, the proper value of 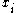 will be computed. Therefore the probability
will be computed. Therefore the probability 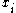 is decoded properly is at least
is decoded properly is at least 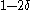 . Therefore,
. Therefore, 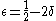 and for
and for  to be positive,
to be positive, 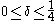 .
.Therefore, the Walsh–Hadamard code is
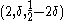 locally decodable for
locally decodable for