
Wagner model
Encyclopedia
Wagner model is a rheological
model developed for the prediction of the viscoelastic
properties of polymers. It might be considered as a simplified practical form of the Bernstein-Kearsley-Zapas model. The model was developed by German rheologist Manfred Wagner
.
For the isothermal
conditions the model can be written as: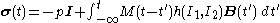
where:
The strain damping function is usually written as: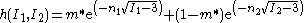 ,
,
The strain hardening function equal to one, then the deformation is small and approaching zero, then the deformations are large.
The Wagner equation can be used in the non-isothermal cases by applying time-temperature shift factor.
Rheology
Rheology is the study of the flow of matter, primarily in the liquid state, but also as 'soft solids' or solids under conditions in which they respond with plastic flow rather than deforming elastically in response to an applied force....
model developed for the prediction of the viscoelastic
Viscoelasticity
Viscoelasticity is the property of materials that exhibit both viscous and elastic characteristics when undergoing deformation. Viscous materials, like honey, resist shear flow and strain linearly with time when a stress is applied. Elastic materials strain instantaneously when stretched and just...
properties of polymers. It might be considered as a simplified practical form of the Bernstein-Kearsley-Zapas model. The model was developed by German rheologist Manfred Wagner
Manfred Wagner
Manfred Hermann Wagner is the author of Wagner model and the molecular stress function theory for polymer rheology.He is a Professor for Polymer engineering and Polymer physics at the Technical University of Berlin....
.
For the isothermal
Isothermal process
An isothermal process is a change of a system, in which the temperature remains constant: ΔT = 0. This typically occurs when a system is in contact with an outside thermal reservoir , and the change occurs slowly enough to allow the system to continually adjust to the temperature of the reservoir...
conditions the model can be written as:
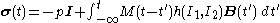
where:
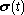 is the stressStress (physics)In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
is the stressStress (physics)In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
tensorTensorTensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
as function of time t,- p is the pressure
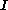 is the unity tensor
is the unity tensor- M is the memory function showing, usually expressed as a sum of exponential terms for each mode of relaxation:
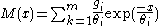 , where for each mode of the relaxation,
, where for each mode of the relaxation,  is the relaxation modulus and
is the relaxation modulus and 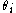 is the relaxation time;
is the relaxation time; 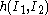 is the strain damping function that depends upon the first and second invariantsInvariants of tensorsIn mathematics, in the fields of multilinear algebra and representation theory, invariants of tensors are coefficients of the characteristic polynomial of the tensor A:\ p:=\det ,...
is the strain damping function that depends upon the first and second invariantsInvariants of tensorsIn mathematics, in the fields of multilinear algebra and representation theory, invariants of tensors are coefficients of the characteristic polynomial of the tensor A:\ p:=\det ,...
of Finger tensor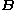 .
.
The strain damping function is usually written as:
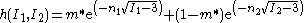 ,
,The strain hardening function equal to one, then the deformation is small and approaching zero, then the deformations are large.
The Wagner equation can be used in the non-isothermal cases by applying time-temperature shift factor.

