
Volume viscosity
Encyclopedia
Volume viscosity becomes important only for such effects where fluid compressibility is essential. Examples would include shock wave
s and sound
propagation. It appears in the Stokes' law (sound attenuation) that describes propagation of sound in Newtonian liquid.
of the stress
tensor
is often identified with the thermodynamic pressure
,
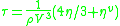
which only depends upon the equilibrium state potentials like temperature and density (equation of state
). In general, the trace of the stress tensor is the sum of thermodynamic pressure contribution plus another contribution which is proportional to the divergence of the velocity field. This constant of proportionality is called the volume viscosity.
Volume viscosity appears in the Navier-Stokes equation if it is written for compressible fluid, as described in the most books on general hydrodynamics , , and acoustics ,.
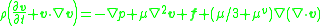
where μv is the volume viscosity coefficient. Authors who use the alternative term bulk viscosity for the same parameter include , . This additional term disappears for incompressible fluid, when the divergence
of the flow equals 0.
This viscosity parameter is additional to the usual dynamic viscosity μ.
at high frequencies. The only values for the volume viscosity of simple Newtonian liquids known to us come from the old Litovitz and Davis review, see References. They report the volume viscosity of water at 15 °C is 3.09 centipoise
Modern Acoustic rheometer
s are able to measure this parameter, see External links.
Shock wave
A shock wave is a type of propagating disturbance. Like an ordinary wave, it carries energy and can propagate through a medium or in some cases in the absence of a material medium, through a field such as the electromagnetic field...
s and sound
Sound
Sound is a mechanical wave that is an oscillation of pressure transmitted through a solid, liquid, or gas, composed of frequencies within the range of hearing and of a level sufficiently strong to be heard, or the sensation stimulated in organs of hearing by such vibrations.-Propagation of...
propagation. It appears in the Stokes' law (sound attenuation) that describes propagation of sound in Newtonian liquid.
Derivation and Use
The negative-one-third of the traceTrace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
of the stress
Stress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
is often identified with the thermodynamic pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
,
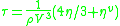
which only depends upon the equilibrium state potentials like temperature and density (equation of state
Equation of state
In physics and thermodynamics, an equation of state is a relation between state variables. More specifically, an equation of state is a thermodynamic equation describing the state of matter under a given set of physical conditions...
). In general, the trace of the stress tensor is the sum of thermodynamic pressure contribution plus another contribution which is proportional to the divergence of the velocity field. This constant of proportionality is called the volume viscosity.
Volume viscosity appears in the Navier-Stokes equation if it is written for compressible fluid, as described in the most books on general hydrodynamics , , and acoustics ,.
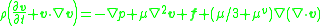
where μv is the volume viscosity coefficient. Authors who use the alternative term bulk viscosity for the same parameter include , . This additional term disappears for incompressible fluid, when the divergence
Divergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
of the flow equals 0.
This viscosity parameter is additional to the usual dynamic viscosity μ.
Measurement
The volume viscosity of many fluids is inaccurately known, despite its fundamental role for fluid dynamicsFluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
at high frequencies. The only values for the volume viscosity of simple Newtonian liquids known to us come from the old Litovitz and Davis review, see References. They report the volume viscosity of water at 15 °C is 3.09 centipoise
Modern Acoustic rheometer
Acoustic rheometer
An acoustic rheometer employs piezo-electric crystal that can easily launch a successive wave of extensions and contractions into the fluid. It applies an oscillating extensional stress to the system...
s are able to measure this parameter, see External links.

