
Volume entropy
Encyclopedia
The volume entropy is an asymptotic invariant
of a compact
Riemannian manifold
that measures the exponential growth rate of the volume of metric balls in its universal cover. This concept is closely related with other notions of entropy
found in dynamical systems and plays an important role in differential geometry and geometric group theory
. If the manifold is nonpositively curved then its volume entropy coincides with the topological entropy
of the geodesic flow. It is of considerable interest in differential geometry to find the Riemannian metric on a given smooth manifold which minimizes the volume entropy, with locally symmetric spaces forming a basic class of examples.
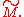 Choose a point
Choose a point 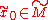 .
.
The volume entropy (or asymptotic volume growth)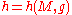 is defined as the limit
is defined as the limit
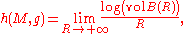
where B(R) is the ball of radius R in centered at
centered at  and vol is the Riemannian volume in the universal cover with the natural Riemannian metric.
and vol is the Riemannian volume in the universal cover with the natural Riemannian metric.
A. Manning proved that the limit exists and does not depend on the choice of the base point. This asymptotic invariant describes the exponential growth rate of the volume of balls in the universal cover as a function of the radius.
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
of a compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
that measures the exponential growth rate of the volume of metric balls in its universal cover. This concept is closely related with other notions of entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
found in dynamical systems and plays an important role in differential geometry and geometric group theory
Geometric group theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
. If the manifold is nonpositively curved then its volume entropy coincides with the topological entropy
Topological entropy
In mathematics, the topological entropy of a topological dynamical system is a nonnegative real number that measures the complexity of the system. Topological entropy was first introduced in 1965 by Adler, Konheim and McAndrew. Their definition was modelled after the definition of the...
of the geodesic flow. It is of considerable interest in differential geometry to find the Riemannian metric on a given smooth manifold which minimizes the volume entropy, with locally symmetric spaces forming a basic class of examples.
Definition
Let (M, g) be a compact Riemannian manifold, with universal cover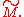 Choose a point
Choose a point 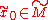 .
.The volume entropy (or asymptotic volume growth)
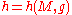 is defined as the limit
is defined as the limit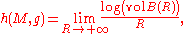
where B(R) is the ball of radius R in
 centered at
centered at  and vol is the Riemannian volume in the universal cover with the natural Riemannian metric.
and vol is the Riemannian volume in the universal cover with the natural Riemannian metric.A. Manning proved that the limit exists and does not depend on the choice of the base point. This asymptotic invariant describes the exponential growth rate of the volume of balls in the universal cover as a function of the radius.
Properties
- Volume entropy h is always bounded above by the topological entropy htop of the geodesic flow on M. Moreover, if M has nonpositive sectional curvature then h = htop. These results are due to Manning.
- More generally, volume entropy equals topological entropy under a weaker assumption that M is a closed Riemannian manifold without conjugate pointsConjugate pointsIn differential geometry, conjugate points are, roughly, points that can almost be joined by a 1-parameter family of geodesics. For example, on a sphere, the north-pole and south-pole are connected by any meridian.-Definition:...
(Freire and Mañé).
- Locally symmetric spaces minimize entropy when the volume is prescribed. This is a corollary of a very general result due to Besson, Courtois, and Gallot (which also implies Mostow rigidity and its various generalizations due to Corlette, Siu, and ThurstonWilliam ThurstonWilliam Paul Thurston is an American mathematician. He is a pioneer in the field of low-dimensional topology. In 1982, he was awarded the Fields Medal for his contributions to the study of 3-manifolds...
):
-
- Let X and Y be compact oriented connected n-dimensional smooth manifolds and f: Y → X a continuous map of non-zero degree. If g0 is a negatively curved locally symmetric Riemannian metric on X and g is any Riemannian metric on Y then
-
-
-
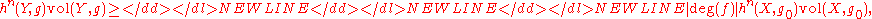
-
- and for n ≥ 3, the equality occurs if and only if (Y,g) is locally symmetric of the same type as (X,g0) and f is homotopic to a homothetic covering (Y,g) → (X,g0).
Application in differential geometry of surfaces
Katok's entropy inequality was recently exploited to obtain a tight asymptotic bound for the systolic ratio of surfaces of large genus, see systoles of surfacesSystoles of surfacesIn mathematics, systolic inequalities for curves on surfaces were first studied by Charles Loewner in 1949 . Given a closed surface, its systole, denoted sys, is defined to the least length of a loop that cannot be contracted to a point on the surface. The systolic area of a metric is defined to...
. -
-
-

