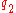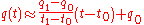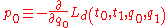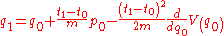Variational integrator
Encyclopedia
Variational integrators are numerical integrators
for Hamiltonian system
s derived from the Euler-Lagrange equations of a discretized Hamilton's principle
. Variational integrators are momentum-preserving and symplectic
.
where is the mass of the particle, and
is the mass of the particle, and  is a potential. To construct a variational integrator for this system, we begin by forming the discrete Lagrangian. The discrete Lagrangian approximates the action for the system over a short time interval:
is a potential. To construct a variational integrator for this system, we begin by forming the discrete Lagrangian. The discrete Lagrangian approximates the action for the system over a short time interval:
Here we have chosen to approximate the time integral using the trapezoid method, and we use a linear approximation to the trajectory,
between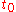 and
and  , resulting in a constant velocity
, resulting in a constant velocity 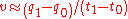 . Different choices for the approximation to the trajectory and the time integral give different variational integrators. The order of accuracy of the integrator is controlled by the accuracy of our approximation to the action; since
. Different choices for the approximation to the trajectory and the time integral give different variational integrators. The order of accuracy of the integrator is controlled by the accuracy of our approximation to the action; since
our integrator will be second-order accurate.
Evolution equations for the discrete system can be derived from a stationary-action principle. The discrete action over an extended time interval is a sum of discrete Lagrangians over many sub-intervals:
The principle of stationary action states that the action is stationary with respect to variations of coordinates that leave the endpoints of the trajectory fixed. So, varying the coordinate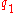 , we have
, we have
Given an initial condition , and a sequence of times
, and a sequence of times 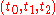 this provides a relation that can be solved for
this provides a relation that can be solved for 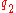 . The solution is
. The solution is
We can write this in a simpler form if we define the discrete momenta,
and
Given an initial condition , the stationary action condition is equivalent to solving the first of these equations for
, the stationary action condition is equivalent to solving the first of these equations for  , and then determining
, and then determining 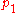 using the second equation. This evolution scheme gives
using the second equation. This evolution scheme gives
and
This is a leapfrog integration
scheme for the system; two steps of this evolution are equivalent to the formula above for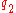
Numerical ordinary differential equations
Numerical ordinary differential equations is the part of numerical analysis which studies the numerical solution of ordinary differential equations...
for Hamiltonian system
Hamiltonian system
In physics and classical mechanics, a Hamiltonian system is a physical system in which forces are momentum invariant. Hamiltonian systems are studied in Hamiltonian mechanics....
s derived from the Euler-Lagrange equations of a discretized Hamilton's principle
Hamilton's principle
In physics, Hamilton's principle is William Rowan Hamilton's formulation of the principle of stationary action...
. Variational integrators are momentum-preserving and symplectic
Symplectic integrator
In mathematics, a symplectic integrator is a numerical integration scheme for a specific group of differential equations related to classical mechanics and symplectic geometry. Symplectic integrators form the subclass of geometric integrators which, by definition, are canonical transformations...
.
Derivation of a Simple Variational Integrator
Consider a mechanical system with a single particle degree of freedom described by the Lagrangian-
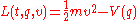 ,
,
where
 is the mass of the particle, and
is the mass of the particle, and  is a potential. To construct a variational integrator for this system, we begin by forming the discrete Lagrangian. The discrete Lagrangian approximates the action for the system over a short time interval:
is a potential. To construct a variational integrator for this system, we begin by forming the discrete Lagrangian. The discrete Lagrangian approximates the action for the system over a short time interval:-
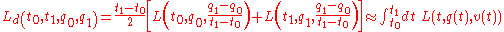 .
.
Here we have chosen to approximate the time integral using the trapezoid method, and we use a linear approximation to the trajectory,
between
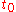 and
and  , resulting in a constant velocity
, resulting in a constant velocity 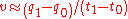 . Different choices for the approximation to the trajectory and the time integral give different variational integrators. The order of accuracy of the integrator is controlled by the accuracy of our approximation to the action; since
. Different choices for the approximation to the trajectory and the time integral give different variational integrators. The order of accuracy of the integrator is controlled by the accuracy of our approximation to the action; since-
 ,
,
our integrator will be second-order accurate.
Evolution equations for the discrete system can be derived from a stationary-action principle. The discrete action over an extended time interval is a sum of discrete Lagrangians over many sub-intervals:
-
 .
.
The principle of stationary action states that the action is stationary with respect to variations of coordinates that leave the endpoints of the trajectory fixed. So, varying the coordinate
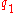 , we have
, we have-
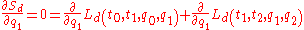 .
.
Given an initial condition
 , and a sequence of times
, and a sequence of times 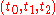 this provides a relation that can be solved for
this provides a relation that can be solved for 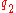 . The solution is
. The solution is-
 .
.
We can write this in a simpler form if we define the discrete momenta,
and
-
 .
.
Given an initial condition
 , the stationary action condition is equivalent to solving the first of these equations for
, the stationary action condition is equivalent to solving the first of these equations for  , and then determining
, and then determining 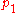 using the second equation. This evolution scheme gives
using the second equation. This evolution scheme givesand
-
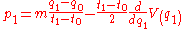 .
.
This is a leapfrog integration
Leapfrog integration
Leapfrog integration is a simple method for numerically integrating differential equations of the form\ddot x=F,or equivalently of the form\dot v=F,\;\dot x \equiv v,particularly in the case of a dynamical system of classical mechanics...
scheme for the system; two steps of this evolution are equivalent to the formula above for