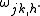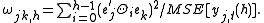Variance decomposition
Encyclopedia
Variance decomposition or forecast error variance decomposition indicates the amount of information each variable contributes to the other variables in a vector autoregression
(VAR) models. Variance decomposition determines how much of the forecast error variance of each of the variable can be explained by exogenous shocks to the other variables.
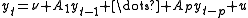 .
.
Change this to a VAR (1) by writing it in companion form (see general matrix notation of a VAR(p))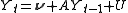 where
where
Vector autoregression
Vector autoregression is a statistical model used to capture the linear interdependencies among multiple time series. VAR models generalize the univariate autoregression models. All the variables in a VAR are treated symmetrically; each variable has an equation explaining its evolution based on...
(VAR) models. Variance decomposition determines how much of the forecast error variance of each of the variable can be explained by exogenous shocks to the other variables.
Calculating the forecast error variance
For the VAR (p) of form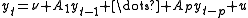 .
.Change this to a VAR (1) by writing it in companion form (see general matrix notation of a VAR(p))
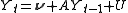 where
where-
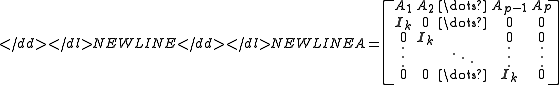 ,
, 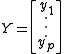 ,
, 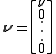 and
and 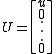
where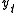 ,
,  and
and  are
are 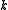 dimensional column vectors,
dimensional column vectors, 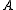 is
is 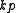 by
by 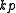 dimensional matrix and
dimensional matrix and  ,
, 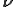 and
and 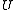 are
are 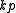 dimensional column vectors.
dimensional column vectors.
Calculate the mean squared error of the h-step forecast of variable j,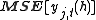 ,
,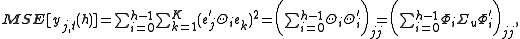
where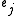 is the jth column of
is the jth column of 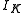 and the subscript
and the subscript 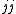 refers to that element of the matrix.
refers to that element of the matrix. 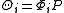 where
where 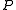 is a lower triangular matrix obtained by a Cholesky decompositionCholesky decompositionIn linear algebra, the Cholesky decomposition or Cholesky triangle is a decomposition of a Hermitian, positive-definite matrix into the product of a lower triangular matrix and its conjugate transpose. It was discovered by André-Louis Cholesky for real matrices...
is a lower triangular matrix obtained by a Cholesky decompositionCholesky decompositionIn linear algebra, the Cholesky decomposition or Cholesky triangle is a decomposition of a Hermitian, positive-definite matrix into the product of a lower triangular matrix and its conjugate transpose. It was discovered by André-Louis Cholesky for real matrices...
of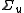 such that
such that 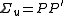 .
. 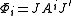 where
where 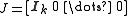 so
so 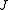 is
is 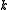 by
by 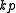 dimensional matrix.
dimensional matrix. 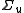 is the covariance matrix of the errors
is the covariance matrix of the errors  .
.
The amount of forecast error variance of variable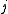 accounted for by exogenous shocks to variable
accounted for by exogenous shocks to variable 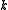 is given by
is given by