
Variable kernel density estimation
Encyclopedia
In statistics
, adaptive or "variable-bandwidth" kernel density estimation is a form of kernel density estimation
in which the size of the kernels used in the estimate are varied
depending upon either the location of the samples or the location of the test point.
It is a particularly effective technique when the sample space is multi-dimensional.
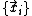 , we wish to estimate the
, we wish to estimate the
density,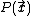 , at a test point,
, at a test point, 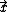 :
:
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, adaptive or "variable-bandwidth" kernel density estimation is a form of kernel density estimation
Kernel density estimation
In statistics, kernel density estimation is a non-parametric way of estimating the probability density function of a random variable. Kernel density estimation is a fundamental data smoothing problem where inferences about the population are made, based on a finite data sample...
in which the size of the kernels used in the estimate are varied
depending upon either the location of the samples or the location of the test point.
It is a particularly effective technique when the sample space is multi-dimensional.
Rationale
Given a set of samples,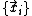 , we wish to estimate the
, we wish to estimate thedensity,
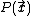 , at a test point,
, at a test point, 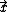 :
:-
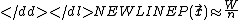
-
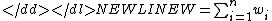
-
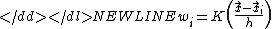
where n is the number of samples, K is the
"kernel"Kernel (statistics)A kernel is a weighting function used in non-parametric estimation techniques. Kernels are used in kernel density estimation to estimate random variables' density functions, or in kernel regression to estimate the conditional expectation of a random variable. Kernels are also used in time-series,...
and
h is its width. The kernel can be thought of as a simple,
linear filterLinear filterLinear filters in the time domain process time-varying input signals to produce output signals, subject to the constraint of linearity.This results from systems composed solely of components classified as having a linear response....
.
Using a fixed filter width may mean that in regions of low density, all samples
will fall in the tails of the filter with very low weighting, while regions of high
density will find an excessive number of samples in the central region with weighting
close to unity. To fix this problem, we vary the width of the kernel in different
regions of the sample space.
There are two methods of doing this: balloon and pointwise estimation.
In a balloon estimator, the kernel width is varied depending on the location
of the test point. In a pointwise estimator, the kernel width is varied depending
on the location of the sample.
For multivariate estimators, the parameter, h, can be generalized to
vary not just the size, but also the shape of the kernel. This more complicated approach
will not be covered here.
Balloon estimators
A common method of varying the kernel width is to make it proportional to the density at the test point:
-
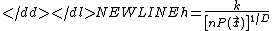
where k is a constant and D is the number of dimensions.
If we back-substitute the estimated PDF,
it is easy to show that W is a constant:
-
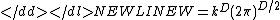
This produces a generalization of the k-nearest neighbour algorithm.
That is, a uniform kernel functionKernel (statistics)A kernel is a weighting function used in non-parametric estimation techniques. Kernels are used in kernel density estimation to estimate random variables' density functions, or in kernel regression to estimate the conditional expectation of a random variable. Kernels are also used in time-series,...
will return the
KNN technique.
There are two components to the error: a variance term and a bias term. The variance term is given as:
-
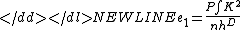 .
.
The bias term is found by evaluating the approximated function in the limit as the kernel
width becomes much larger than the sample spacing. By using a Taylor expansion for the real function, the bias term drops out:
-
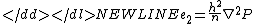
An optimal kernel width that minimizes the error of each estimate can thus be derived.
Use for statistical classification
The method is particularly effective when applied to statistical classification.
There are two ways we can proceed: the first is to compute the PDFs of
each class separately, using different bandwidth parameters,
and then compare them as in Taylor.
Alternatively, we can divide up the sum based on the class of each sample:
-
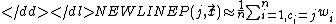
where ci is the class of the ith sample.
The class of the test point may be estimated through maximum likelihoodMaximum likelihoodIn statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
.
Many kernels, Gaussian for instance, are smooth. Consequently, estimates
of joint or conditional probabilities are both continuous and differentiable.
This makes it easy to search for a border between two classes by zeroing
the difference between the conditional probabilities:
-

For example, we can use a one-dimensional root-finding algorithmRoot-finding algorithmA root-finding algorithm is a numerical method, or algorithm, for finding a value x such that f = 0, for a given function f. Such an x is called a root of the function f....
to zero
R along a line between two samples that straddle the class border.
The border can be thus sampled as many times as necessary.
The border samples along with estimates of the gradients of R
determine the class of a test point through a dot-product:
-
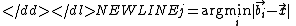
-
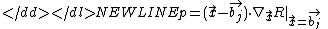
-
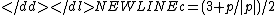
where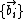 sample the
sample the
class border and c is the estimated class.
The value of R, which determines the conditional probabilities,
may be extrapolated to the test point:
-

Two-class classifications are easy to generalize to multiple classes.
External links
- libAGF - A library for multivariate, adaptive kernel density estimation.
-
-
-
-
-
-
-
-
-
-
-
-

