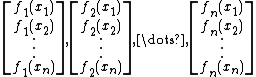Unisolvent functions
Encyclopedia
In mathematics, a collection of n functions ƒ1, ƒ2, ..., ƒn is unisolvent on domain Ω if the vectors
are linearly independent for any choice of n distinct points x1, x2 ... xn in Ω. Equivalently, the collection is unisolvent if the matrix F with entries ƒi(xj) has nonzero determinant: det(F) ≠ 0 for any choice of distinct xj's in Ω.
Unisolvent systems of functions are widely used in interpolation
since they guarantee a unique solution to the interpolation problem. Polynomial
s are unisolvent by the unisolvence theorem
Examples:
Systems of unisolvent functions are much more common in 1 dimension than in higher dimensions. In dimension d = 2 and higher (Ω ⊂ Rd), the functions ƒ1, ƒ2, ..., ƒn cannot be unisolvent on Ω if there exists a single open set on which they are all continuous. To see this, consider moving points x1 and x2 along continuous paths in the open set until they have switched positions, such that x1 and x2 never intersect each other or any of the other xi. The determinant of the resulting system (with x1 and x2 swapped) is the negative of the determinant of the initial system. Since the functions ƒi are continuous, the intermediate value theorem
implies that some intermediate configuration has determinant zero, hence the functions cannot be unisolvent.
are linearly independent for any choice of n distinct points x1, x2 ... xn in Ω. Equivalently, the collection is unisolvent if the matrix F with entries ƒi(xj) has nonzero determinant: det(F) ≠ 0 for any choice of distinct xj's in Ω.
Unisolvent systems of functions are widely used in interpolation
Interpolation
In the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
since they guarantee a unique solution to the interpolation problem. Polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s are unisolvent by the unisolvence theorem
Examples:
- 1, x, x2 is unisolvent on any interval by the unisolvence theorem
- 1, x2 is unisolvent on [0, 1], but not unisolvent on [−1, 1]
- 1, cos(x), cos(2x), ..., cos(nx), sin(x), sin(2x), ..., sin(nx) is unisolvent on [−π, π]
Systems of unisolvent functions are much more common in 1 dimension than in higher dimensions. In dimension d = 2 and higher (Ω ⊂ Rd), the functions ƒ1, ƒ2, ..., ƒn cannot be unisolvent on Ω if there exists a single open set on which they are all continuous. To see this, consider moving points x1 and x2 along continuous paths in the open set until they have switched positions, such that x1 and x2 never intersect each other or any of the other xi. The determinant of the resulting system (with x1 and x2 swapped) is the negative of the determinant of the initial system. Since the functions ƒi are continuous, the intermediate value theorem
Intermediate value theorem
In mathematical analysis, the intermediate value theorem states that for each value between the least upper bound and greatest lower bound of the image of a continuous function there is at least one point in its domain that the function maps to that value....
implies that some intermediate configuration has determinant zero, hence the functions cannot be unisolvent.