
Unique prime
Encyclopedia
In number theory
, a unique prime is a certain kind of prime number
. A prime p ≠ 2, 5 is called unique if there is no other prime q such that the period length of the decimal expansion of its reciprocal, 1 / p, is equivalent to the period length of the reciprocal of q, 1 / q. Unique primes were first described by Samuel Yates
in 1980.
It can be shown that a prime p is of unique period n if and only if
there exists a natural number
c such that
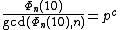
where Φn(x) is the n-th cyclotomic polynomial
. At present, more than fifty unique primes or probable prime
s are known. However, there are only twenty-three unique primes below 10100. The following table gives an overview of all 23 unique primes below 10100 and their periods :
The prime with period length 294 is similar to the reciprocal of 7 (0.142857142857142857...)
Just after the table, the twenty-fourth unique prime has 128 digits and period length 320. It can be written as (932032)2 + 1, where a subscript number n indicates n consecutive copies of the digit or group of digits before the subscript.
Though they are rare, based on the occurrence of repunit
primes and probable primes, it is conjecture
d strongly that there are infinitely many unique primes. (Any repunit prime is unique.)
the repunit (10270343-1)/9 is the largest known probable unique prime.
In 1996 the largest proven unique prime was (101132 + 1)/10001 or, using the notation above, (99990000)141+ 1. Its reciprocal period is 2264. The record has been improved many times since then. the largest proven unique prime has 10,081 digits.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, a unique prime is a certain kind of prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
. A prime p ≠ 2, 5 is called unique if there is no other prime q such that the period length of the decimal expansion of its reciprocal, 1 / p, is equivalent to the period length of the reciprocal of q, 1 / q. Unique primes were first described by Samuel Yates
Samuel Yates
Samuel Yates was a mathematician who first described unique primes in the 1980s. In 1984 he began the list of "Largest Known Primes" and coined the name titanic prime for any prime with 1,000 or more decimal digits...
in 1980.
It can be shown that a prime p is of unique period n if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
there exists a natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
c such that
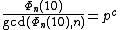
where Φn(x) is the n-th cyclotomic polynomial
Cyclotomic polynomial
In algebra, the nth cyclotomic polynomial, for any positive integer n, is the monic polynomial:\Phi_n = \prod_\omega \,where the product is over all nth primitive roots of unity ω in a field, i.e...
. At present, more than fifty unique primes or probable prime
Probable prime
In number theory, a probable prime is an integer that satisfies a specific condition also satisfied by all prime numbers. Different types of probable primes have different specific conditions...
s are known. However, there are only twenty-three unique primes below 10100. The following table gives an overview of all 23 unique primes below 10100 and their periods :
| Period length | Prime |
|---|---|
| 1 | 3 |
| 2 | 11 11 (number) 11 is the natural number following 10 and preceding 12.Eleven is the first number which cannot be counted with a human's eight fingers and two thumbs additively. In English, it is the smallest positive integer requiring three syllables and the largest prime number with a single-morpheme name... |
| 3 | 37 37 (number) 37 is the natural number following 36 and preceding 38.-In mathematics:It is a prime number, the fifth lucky prime, the first irregular prime, the third unique prime and the third cuban prime of the form... |
| 4 | 101 101 (number) 101 is the natural number following 100 and preceding 102.It is variously pronounced "one hundred and one" / "a hundred and one", "one hundred one" / "a hundred one", and "one oh one"... |
| 10 | 9,091 |
| 12 | 9,901 |
| 9 | 333,667 |
| 14 | 909,091 |
| 24 | 99,990,001 |
| 36 | 999,999,000,001 |
| 48 | 9,999,999,900,000,001 |
| 38 | 909,090,909,090,909,091 |
| 19 | 1,111,111,111,111,111,111 |
| 23 | 11,111,111,111,111,111,111,111 |
| 39 | 900,900,900,900,990,990,990,991 |
| 62 | 909,090,909,090,909,090,909,090,909,091 |
| 120 | 100,009,999,999,899,989,999,000,000,010,001 |
| 150 | 10,000,099,999,999,989,999,899,999,000,000,000,100,001 |
| 106 | 9,090,909,090,909,090,909,090,909,090,909,090,909,090,909,090,909,091 |
| 93 | 900,900,900,900,900,900,900,900,900,900,990,990,990,990,990,990,990,990,990,991 |
| 134 | 909,090,909,090,909,090,909,090,909,090,909,090,909,090,909,090,909,090,909,090,909,091 |
| 294 | 142,857,157,142,857,142,856,999,999,985,714,285,714,285,857,142,857,142,855,714,285,571,428,571,428,572,857,143 |
| 196 | 999,999,999,999,990,000,000,000,000,099,999,999,999,999,000,000,000,000,009,999,999,999,999,900,000,000,000,001 |
The prime with period length 294 is similar to the reciprocal of 7 (0.142857142857142857...)
Just after the table, the twenty-fourth unique prime has 128 digits and period length 320. It can be written as (932032)2 + 1, where a subscript number n indicates n consecutive copies of the digit or group of digits before the subscript.
Though they are rare, based on the occurrence of repunit
Repunit
In recreational mathematics, a repunit is a number like 11, 111, or 1111 that contains only the digit 1. The term stands for repeated unit and was coined in 1966 by Albert H. Beiler...
primes and probable primes, it is conjecture
Conjecture
A conjecture is a proposition that is unproven but is thought to be true and has not been disproven. Karl Popper pioneered the use of the term "conjecture" in scientific philosophy. Conjecture is contrasted by hypothesis , which is a testable statement based on accepted grounds...
d strongly that there are infinitely many unique primes. (Any repunit prime is unique.)
the repunit (10270343-1)/9 is the largest known probable unique prime.
In 1996 the largest proven unique prime was (101132 + 1)/10001 or, using the notation above, (99990000)141+ 1. Its reciprocal period is 2264. The record has been improved many times since then. the largest proven unique prime has 10,081 digits.

