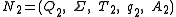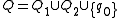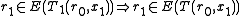Union of two regular languages
Encyclopedia
In formal language
theory, and in particular the theory of nondeterministic finite state machine
s, it is known that the union of two regular languages is a regular language
. This article provides a proof of that statement.
and 
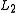, language 
is regular.
Proof
Since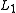
and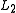 
are regular, there exist NFAs
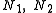that recognize 
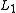and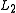 
.
Let
Construct
where
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
theory, and in particular the theory of nondeterministic finite state machine
Nondeterministic finite state machine
In the automata theory, a nondeterministic finite state machine or nondeterministic finite automaton is a finite state machine where from each state and a given input symbol the automaton may jump into several possible next states...
s, it is known that the union of two regular languages is a regular language
Regular language
In theoretical computer science and formal language theory, a regular language is a formal language that can be expressed using regular expression....
. This article provides a proof of that statement.
Theorem
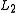For any regular languages and , language is regular.Proof
Since
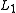and 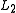are regular, there exist NFAsNondeterministic finite state machine
In the automata theory, a nondeterministic finite state machine or nondeterministic finite automaton is a finite state machine where from each state and a given input symbol the automaton may jump into several possible next states...
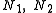that recognize 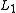and 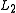.Let
Construct
where
-
In the following, we shall use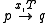
to denote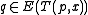 
Let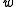
be a string from 
. Without loss of generalityWithout loss of generalityWithout loss of generality is a frequently used expression in mathematics...
assume
.
Let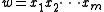
where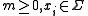 
Since
accepts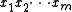 
, there exist 
such that
-
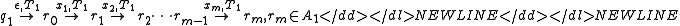
Since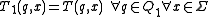
We can therefore substitute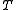
for 
and rewrite the above path as
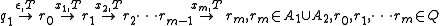
Furthermore,
-
-
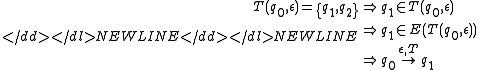
and
-
-
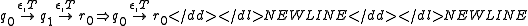
The above path can be rewritten as
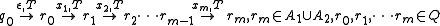
Therefore,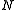
accepts 
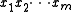and the proof is complete.
Note: The idea drawn from this mathematical proof for constructing a machine to recognize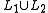
is to create an initial state and connect it to the initial states of 
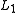and 
using 
arrows.
-
-
-
-
-
