
Uncertainty coefficient
Encyclopedia
In statistics
, the uncertainty coefficient, also called entropy coefficient or Theil's U, is a measure of nominal association
. It was first introduced by Henri Theil
and is based on the concept of information entropy
. Suppose we have samples of two (normally discrete) random variables, i and j. By constructing the joint distribution, P(i, j), from which we can calculate the conditional distributions, P(i|j) = P(i, j)/P(j) and P(j|i) = P(i, j)/P(i), and calculating the various entropies, we can determine the degree of association between the two variables.
The entropy of a single distribution is given as
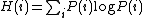
while the conditional entropy is given as:
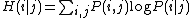
The uncertainty coefficient is defined as

and tells us: given j, what fraction of the bits of i can we predict? In this case we can think of i as containing the "true" values. The measure can be inverted to return the reverse question and a symmetrical measure thus defined as a weighted average between the two:

The uncertainty coefficient is useful for measuring the validity of a statistical classification algorithm and has the advantage over simple accuracy in that it is not affected by the relative fractions of the different classes, i.e., P(i)
.
It also has the unique property that it won't penalize an algorithm for predicting the wrong classes, so long as it does so consistently (i.e., it simply rearranges the classes). Although normally applied to discrete variables, it can be extended to continuous variables using density estimation
.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the uncertainty coefficient, also called entropy coefficient or Theil's U, is a measure of nominal association
Association (statistics)
In statistics, an association is any relationship between two measured quantities that renders them statistically dependent. The term "association" refers broadly to any such relationship, whereas the narrower term "correlation" refers to a linear relationship between two quantities.There are many...
. It was first introduced by Henri Theil
Henri Theil
Henri Theil was a Dutch econometrician.He graduated from the University of Amsterdam. He was the successor of Jan Tinbergen at the Erasmus University Rotterdam. Later he taught in Chicago and at the University of Florida. He is most famous for his invention of 2-stage least squares...
and is based on the concept of information entropy
Information entropy
In information theory, entropy is a measure of the uncertainty associated with a random variable. In this context, the term usually refers to the Shannon entropy, which quantifies the expected value of the information contained in a message, usually in units such as bits...
. Suppose we have samples of two (normally discrete) random variables, i and j. By constructing the joint distribution, P(i, j), from which we can calculate the conditional distributions, P(i|j) = P(i, j)/P(j) and P(j|i) = P(i, j)/P(i), and calculating the various entropies, we can determine the degree of association between the two variables.
The entropy of a single distribution is given as
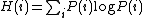
while the conditional entropy is given as:
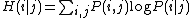
The uncertainty coefficient is defined as

and tells us: given j, what fraction of the bits of i can we predict? In this case we can think of i as containing the "true" values. The measure can be inverted to return the reverse question and a symmetrical measure thus defined as a weighted average between the two:

The uncertainty coefficient is useful for measuring the validity of a statistical classification algorithm and has the advantage over simple accuracy in that it is not affected by the relative fractions of the different classes, i.e., P(i)
.
It also has the unique property that it won't penalize an algorithm for predicting the wrong classes, so long as it does so consistently (i.e., it simply rearranges the classes). Although normally applied to discrete variables, it can be extended to continuous variables using density estimation
Density estimation
In probability and statistics,density estimation is the construction of an estimate, based on observed data, of an unobservable underlying probability density function...
.
External links
- Nominal Association: Phi, Contingency Coefficient, Tschuprow's T, Cramer's V, Lambda, Uncertainty Coefficient Course notes, 2008 by G. David Garson, NCSU

