
Two-balloon experiment
Encyclopedia
The two-balloon experiment is a simple experiment involving interconnected balloon
s. It is used in physics classes as a demonstration of elasticity
.
Two identical balloons are inflated to different diameters and connected together by means of a tube. The flow of air through the tube is controlled by a valve or clamp. The clamp is then released, allowing air to flow between the balloons. For many starting conditions, the smaller balloon then gets smaller and the balloon with the larger diameter inflates even more. This result is surprising, since most people assume that the two balloons will have equal sizes after exchanging air.
However, the outcome may vary depending on the initial sizes and elastic properties of the balloons involved. This makes even a system with idealised rubber balloons more complex than an equivalent with, say, soap bubbles. In addition, natural rubber exhibits hysteresis
effects, and so what appears a simple experiment can produce extremely complex behaviour. The system has been modelled by a number of authors, for example to produce phase diagrams specifying under what conditions the small balloon can inflates the larger, or the other way round.
The James-Guth
stress-strain relation
for a parallelepiped
of ideal rubber can be written

Here,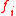 is the externally applied force in the
is the externally applied force in the  direction,
direction,
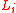 is a linear dimension,
is a linear dimension,  is Boltzmann's constant,
is Boltzmann's constant,
 is a constant related to the number of possible network configurations of the sample,
is a constant related to the number of possible network configurations of the sample,  is the absolute temperature,
is the absolute temperature,
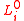 is an unstretched dimension,
is an unstretched dimension, 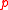 is the internal (hydrostatic) pressure
is the internal (hydrostatic) pressure
, and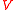 is the volume of the sample. Thus, the force consists of two parts: the first one (caused by the polymer network) gives a tendency to contract, while the second gives a tendency to expand.
is the volume of the sample. Thus, the force consists of two parts: the first one (caused by the polymer network) gives a tendency to contract, while the second gives a tendency to expand.
Suppose that the balloon is composed of many such interconnected patches, which deform in a similar way as the balloon expands. Because rubber strongly resists volume changes,the volume can be considered constant. This allows the stress-strain relation to be written
can be considered constant. This allows the stress-strain relation to be written
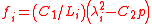
where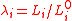 is the relative extension. In the case of a thin-walled spherical shell, all the force which acts to stretch the rubber is directed tangentially to the surface. The radial force (i.e., the force acting to compress the shell wall) can therefore be set equal to zero, so that
is the relative extension. In the case of a thin-walled spherical shell, all the force which acts to stretch the rubber is directed tangentially to the surface. The radial force (i.e., the force acting to compress the shell wall) can therefore be set equal to zero, so that

where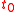 and
and  refer to the initial and final thicknesses, respectively. For a balloon of radius
refer to the initial and final thicknesses, respectively. For a balloon of radius  , a fixed volume of rubber means that
, a fixed volume of rubber means that  is constant, or equivalently
is constant, or equivalently

hence
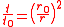
and the radial force equation becomes

The equation for the tangential force (where
(where 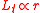 ) then becomes
) then becomes

Integrating the internal air pressure over one hemisphere of the balloon then gives
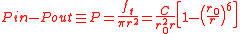
where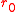 is the balloon's uninflated radius.
is the balloon's uninflated radius.
This equation is plotted in the figure at left. The internal pressure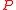 reaches a maximum for
reaches a maximum for
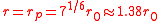
and drops to zero as increases. This behavior is well known to anyone who has blown up a balloon: a large force is required at the start, but after the balloon expands (to a radius larger than
increases. This behavior is well known to anyone who has blown up a balloon: a large force is required at the start, but after the balloon expands (to a radius larger than 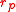 ), less force is needed for continued inflation.
), less force is needed for continued inflation.
 ) and one on the right branch (
) and one on the right branch (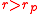 ).
).
Equilibria are also possible in which both balloons have the same size. If the total quantity of air in both balloons is less than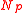 , defined as the number of molecules in both balloons if they both sit at the peak of the pressure curve, then both balloons settle down to the left of the pressure peak with the same radius,
, defined as the number of molecules in both balloons if they both sit at the peak of the pressure curve, then both balloons settle down to the left of the pressure peak with the same radius,  . On the other hand, if the total number of molecules exceeds
. On the other hand, if the total number of molecules exceeds 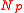 , the only possible equilibrium state is the one described above, with one balloon on the left of the peak and one on the right. Equilibria in which both balloons are on the right of the pressure peak also exist but are unstable.This is easy to verify by squeezing the air back and forth between two interconnected balloons.
, the only possible equilibrium state is the one described above, with one balloon on the left of the peak and one on the right. Equilibria in which both balloons are on the right of the pressure peak also exist but are unstable.This is easy to verify by squeezing the air back and forth between two interconnected balloons.
, imperfect flexibility of the molecular chains, steric hindrances
and the like. As a result, if the two balloons are initially very extended, other outcomes of the two-balloon experiment are possible.
Real balloons also experience hysteresis: the pressure depends not just on the balloon diameter, but also on the manner in which inflation took place and on the initial direction of change. For instance, the pressure during inflation is always greater than the pressure during subsequent deflation at a given radius. One consequence is that equilibrium will generally be obtained with a lesser change in diameter than would have occurred in the ideal case.
Balloon
A balloon is an inflatable flexible bag filled with a gas, such as helium, hydrogen, nitrous oxide, oxygen, or air. Modern balloons can be made from materials such as rubber, latex, polychloroprene, or a nylon fabric, while some early balloons were made of dried animal bladders, such as the pig...
s. It is used in physics classes as a demonstration of elasticity
Elasticity
Elasticity may refer to:*Elasticity , continuum mechanics of bodies that deform reversibly under stressNumerous uses are derived from this physical sense of the term, which is inherently mathematical, such as used in Engineering, Chemistry, Construction and variously in Economics:*Elasticity , the...
.
Two identical balloons are inflated to different diameters and connected together by means of a tube. The flow of air through the tube is controlled by a valve or clamp. The clamp is then released, allowing air to flow between the balloons. For many starting conditions, the smaller balloon then gets smaller and the balloon with the larger diameter inflates even more. This result is surprising, since most people assume that the two balloons will have equal sizes after exchanging air.
However, the outcome may vary depending on the initial sizes and elastic properties of the balloons involved. This makes even a system with idealised rubber balloons more complex than an equivalent with, say, soap bubbles. In addition, natural rubber exhibits hysteresis
Hysteresis
Hysteresis is the dependence of a system not just on its current environment but also on its past. This dependence arises because the system can be in more than one internal state. To predict its future evolution, either its internal state or its history must be known. If a given input alternately...
effects, and so what appears a simple experiment can produce extremely complex behaviour. The system has been modelled by a number of authors, for example to produce phase diagrams specifying under what conditions the small balloon can inflates the larger, or the other way round.
Theoretical pressure curve
The key to understanding the behavior of the balloons is understanding how the pressure inside a balloon varies with the balloon's diameter. The simplest way to do this is to imagine that the balloon is made up of a large number of small rubber patches, and to analyze how the size of a patch is affected by the force acting on it.The James-Guth
Eugene Guth
Eugene Guth was an American physicist who made contributions to polymer physics and to nuclear and solid state physics. He was awarded a Ph.D. in Theoretical Physics by the University of Vienna in 1928...
stress-strain relation
Stress-strain curve
During tensile testing of a material sample, the stress–strain curve is a graphical representation of the relationship between stress, derived from measuring the load applied on the sample, and strain, derived from measuring the deformation of the sample, i.e. elongation, compression, or distortion...
for a parallelepiped
Parallelepiped
In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms. By analogy, it relates to a parallelogram just as a cube relates to a square. In Euclidean geometry, its definition encompasses all four concepts...
of ideal rubber can be written

Here,
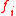 is the externally applied force in the
is the externally applied force in the  direction,
direction,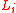 is a linear dimension,
is a linear dimension,  is Boltzmann's constant,
is Boltzmann's constant, is a constant related to the number of possible network configurations of the sample,
is a constant related to the number of possible network configurations of the sample,  is the absolute temperature,
is the absolute temperature,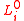 is an unstretched dimension,
is an unstretched dimension, 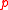 is the internal (hydrostatic) pressure
is the internal (hydrostatic) pressurePressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
, and
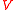 is the volume of the sample. Thus, the force consists of two parts: the first one (caused by the polymer network) gives a tendency to contract, while the second gives a tendency to expand.
is the volume of the sample. Thus, the force consists of two parts: the first one (caused by the polymer network) gives a tendency to contract, while the second gives a tendency to expand.Suppose that the balloon is composed of many such interconnected patches, which deform in a similar way as the balloon expands. Because rubber strongly resists volume changes,the volume
 can be considered constant. This allows the stress-strain relation to be written
can be considered constant. This allows the stress-strain relation to be written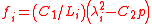
where
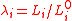 is the relative extension. In the case of a thin-walled spherical shell, all the force which acts to stretch the rubber is directed tangentially to the surface. The radial force (i.e., the force acting to compress the shell wall) can therefore be set equal to zero, so that
is the relative extension. In the case of a thin-walled spherical shell, all the force which acts to stretch the rubber is directed tangentially to the surface. The radial force (i.e., the force acting to compress the shell wall) can therefore be set equal to zero, so that
where
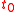 and
and  refer to the initial and final thicknesses, respectively. For a balloon of radius
refer to the initial and final thicknesses, respectively. For a balloon of radius  , a fixed volume of rubber means that
, a fixed volume of rubber means that  is constant, or equivalently
is constant, or equivalently
hence
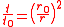
and the radial force equation becomes

The equation for the tangential force
 (where
(where 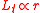 ) then becomes
) then becomes
Integrating the internal air pressure over one hemisphere of the balloon then gives
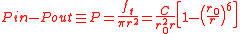
where
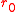 is the balloon's uninflated radius.
is the balloon's uninflated radius.This equation is plotted in the figure at left. The internal pressure
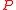 reaches a maximum for
reaches a maximum for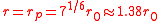
and drops to zero as
 increases. This behavior is well known to anyone who has blown up a balloon: a large force is required at the start, but after the balloon expands (to a radius larger than
increases. This behavior is well known to anyone who has blown up a balloon: a large force is required at the start, but after the balloon expands (to a radius larger than 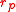 ), less force is needed for continued inflation.
), less force is needed for continued inflation.Why the larger balloon expands
When the valve is released, air will flow from the balloon at higher pressure to the balloon at lower pressure. The lower pressure balloon will expand. Figure 2 (above left) shows a typical initial configuration: the smaller balloon has the higher pressure. So, when the valve is opened, the smaller balloon pushes air into the larger balloon. It becomes smaller, and the larger balloon becomes larger. The air flow ceases when the two balloons have equal pressure, with one on the left branch of the pressure curve ( ) and one on the right branch (
) and one on the right branch (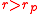 ).
).Equilibria are also possible in which both balloons have the same size. If the total quantity of air in both balloons is less than
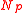 , defined as the number of molecules in both balloons if they both sit at the peak of the pressure curve, then both balloons settle down to the left of the pressure peak with the same radius,
, defined as the number of molecules in both balloons if they both sit at the peak of the pressure curve, then both balloons settle down to the left of the pressure peak with the same radius,  . On the other hand, if the total number of molecules exceeds
. On the other hand, if the total number of molecules exceeds 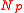 , the only possible equilibrium state is the one described above, with one balloon on the left of the peak and one on the right. Equilibria in which both balloons are on the right of the pressure peak also exist but are unstable.This is easy to verify by squeezing the air back and forth between two interconnected balloons.
, the only possible equilibrium state is the one described above, with one balloon on the left of the peak and one on the right. Equilibria in which both balloons are on the right of the pressure peak also exist but are unstable.This is easy to verify by squeezing the air back and forth between two interconnected balloons.Non-ideal balloons
At large extensions, the pressure inside a natural rubber balloon once again goes up. This is due to a number of physical effects that were ignored in the James/Guth theory: crystallizationStrain crystallization
Strain crystallization is a phenomenon in which an initially amorphous solid material undergoes a phase transformation due to the application of strain. Strain crystallization occurs in natural rubber, and some other elastomers. The phenomenon has important effects on strength and fatigue...
, imperfect flexibility of the molecular chains, steric hindrances
Steric effects
Steric effects arise from the fact that each atom within a molecule occupies a certain amount of space. If atoms are brought too close together, there is an associated cost in energy due to overlapping electron clouds , and this may affect the molecule's preferred shape and reactivity.-Steric...
and the like. As a result, if the two balloons are initially very extended, other outcomes of the two-balloon experiment are possible.
Real balloons also experience hysteresis: the pressure depends not just on the balloon diameter, but also on the manner in which inflation took place and on the initial direction of change. For instance, the pressure during inflation is always greater than the pressure during subsequent deflation at a given radius. One consequence is that equilibrium will generally be obtained with a lesser change in diameter than would have occurred in the ideal case.

