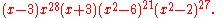Tutte 12-cage
Encyclopedia
In the mathematical
field of graph theory
, the Tutte 12-cage or Benson graph is a 3-regular graph
with 126 vertices and 189 edges named after W. T. Tutte
.
The Tutte 12-cage is the unique (3-12)-cage . It was discovered by C. T. Benson in 1966. It has chromatic number 2 (bipartite
), chromatic index 3, girth 12 (as a 12-cage) and diameter 6. Its crossing number
is 170 and has been conjectured to be the smallest cubic graph with this crossing number.
Hamiltonian graph and can be defined by the LCF notation
[17, 27, –13, –59, –35, 35, –11, 13, –53, 53, –27, 21, 57, 11, –21, –57, 59, –17]7.
It is the incidence graph of the generalized hexagon GH(2,2) with 63 points and 63 lines.
The Balaban 11-cage
can be constructed by excision from the Tutte 12-cage by removing a small subtree and suppressing the resulting vertices of degree two.
Z/2Z. Its acts transitively on its edges but not on its vertices, making it a semi-symmetric graph
, a regular graph that is edge-transitive
but not vertex-transitive
. In fact, the automorphism group of the Tutte 12-cage preserves the bipartite parts and acts primitively on each part. Such graphs are called bi-primitive graphs and only five cubic bi-primitive graphs exist; they are named the Iofinova-Ivanov graphs and are of order 110, 126, 182, 506 and 990.
All the cubic semi-symmetric graphs on up to 768 vertices are known. According to Conder, Malnič, Marušič and Potočnik, the Tutte 12-cage is the unique cubic semi-symmetric graph on 126 vertices and is the fifth smallest possible cubic semi-symmetric graph after the Gray graph
, the Iofinova–Ivanov graph on 110 vertices, the Ljubljana graph
and a graph on 120 vertices with girth 8.
The characteristic polynomial
of the Tutte 12-cage is
It is the only graph with this characteristic polynomial; therefore, the 12-cage is determined by its spectrum
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the Tutte 12-cage or Benson graph is a 3-regular graph
Regular graph
In graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other...
with 126 vertices and 189 edges named after W. T. Tutte
W. T. Tutte
William Thomas Tutte, OC, FRS, known as Bill Tutte, was a British, later Canadian, codebreaker and mathematician. During World War II he made a brilliant and fundamental advance in Cryptanalysis of the Lorenz cipher, a major German code system, which had a significant impact on the Allied...
.
The Tutte 12-cage is the unique (3-12)-cage . It was discovered by C. T. Benson in 1966. It has chromatic number 2 (bipartite
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
), chromatic index 3, girth 12 (as a 12-cage) and diameter 6. Its crossing number
Crossing number (graph theory)
In graph theory, the crossing number cr of a graph G is the lowest number of edge crossings of a planar drawing of the graph G. For instance, a graph is planar if and only if its crossing number is zero.The concept originated in...
is 170 and has been conjectured to be the smallest cubic graph with this crossing number.
Construction
The Tutte 12-cage is a cubicCubic graph
In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs....
Hamiltonian graph and can be defined by the LCF notation
LCF notation
In combinatorial mathematics, LCF notation or LCF code is a notation devised by Joshua Lederberg, and extended by Coxeter and Frucht, for the representation of cubic graphs that are Hamiltonian. Since the graphs are Hamiltonian, the vertices can be arranged in a cycle, which accounts for two edges...
[17, 27, –13, –59, –35, 35, –11, 13, –53, 53, –27, 21, 57, 11, –21, –57, 59, –17]7.
It is the incidence graph of the generalized hexagon GH(2,2) with 63 points and 63 lines.
The Balaban 11-cage
Balaban 11-cage
In the mathematical field of graph theory, the Balaban 11-cage or Balaban -cage is a 3-regular graph with 112 vertices and 168 edges named after A. T. Balaban.The Balaban 11-cage is the unique -cage. It was discovered by Balaban in 1973...
can be constructed by excision from the Tutte 12-cage by removing a small subtree and suppressing the resulting vertices of degree two.
Algebraic properties
The automorphism group of the Tutte 12-cage is of order and is a semi-direct product of the projective special unitary group PSU(3,3) with the cyclic groupCyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
Z/2Z. Its acts transitively on its edges but not on its vertices, making it a semi-symmetric graph
Semi-symmetric graph
In the mathematical field of graph theory, a semi-symmetric graph is an undirected graph that is edge-transitive and regular, but not vertex-transitive....
, a regular graph that is edge-transitive
Edge-transitive graph
In the mathematical field of graph theory, an edge-transitive graph is a graph G such that, given any two edges e1 and e2 of G, there is anautomorphism of G that maps e1 to e2....
but not vertex-transitive
Vertex-transitive graph
In the mathematical field of graph theory, a vertex-transitive graph is a graph G such that, given any two vertices v1 and v2 of G, there is some automorphismf:V \rightarrow V\ such thatf = v_2.\...
. In fact, the automorphism group of the Tutte 12-cage preserves the bipartite parts and acts primitively on each part. Such graphs are called bi-primitive graphs and only five cubic bi-primitive graphs exist; they are named the Iofinova-Ivanov graphs and are of order 110, 126, 182, 506 and 990.
All the cubic semi-symmetric graphs on up to 768 vertices are known. According to Conder, Malnič, Marušič and Potočnik, the Tutte 12-cage is the unique cubic semi-symmetric graph on 126 vertices and is the fifth smallest possible cubic semi-symmetric graph after the Gray graph
Gray graph
In the mathematical field of graph theory, the Gray graph is an undirected bipartite graph with 54 vertices and 81 edges. It is a cubic graph: every vertex touches exactly three edges. It was discovered by Marion C. Gray in 1932 , then discovered independently by Bouwer 1968 in reply to a question...
, the Iofinova–Ivanov graph on 110 vertices, the Ljubljana graph
Ljubljana graph
In the mathematical field of graph theory, the Ljubljana graph is an undirected bipartite graph with 112 vertices and 168 edges.It is a cubic graph with diameter 8, radius 7, chromatic number 2 and chromatic index 3. Its girth is 10 and there are exactly 168 cycles of length 10 in it...
and a graph on 120 vertices with girth 8.
The characteristic polynomial
Characteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
of the Tutte 12-cage is
It is the only graph with this characteristic polynomial; therefore, the 12-cage is determined by its spectrum
Spectral graph theory
In mathematics, spectral graph theory is the study of properties of a graph in relationship to the characteristic polynomial, eigenvalues, and eigenvectors of matrices associated to the graph, such as its adjacency matrix or Laplacian matrix....
.