
Turing machine gallery
Encyclopedia

Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
.
Turing machine as a mechanical device
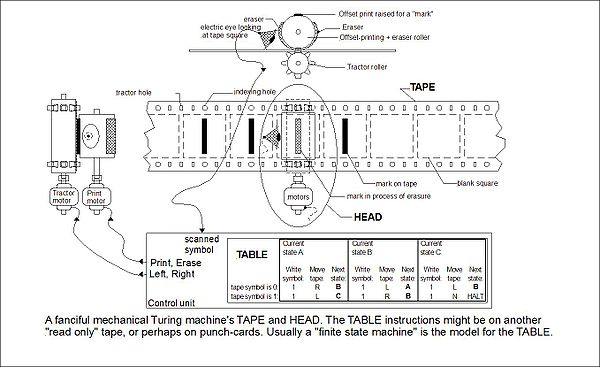
Punched card
A punched card, punch card, IBM card, or Hollerith card is a piece of stiff paper that contains digital information represented by the presence or absence of holes in predefined positions...
s. Turing's biographer Andrew Hodges
Andrew Hodges
Andrew Hodges is a mathematician, an author and a pioneer of the gay liberation movement of the 1970s.For the past decades , Hodges has focused his research activities on the twistor theory — the new approach to the problems of fundamental physics pioneered by the mathematician Roger...
(1983) has written that Turing as a child liked typewriter
Typewriter
A typewriter is a mechanical or electromechanical device with keys that, when pressed, cause characters to be printed on a medium, usually paper. Typically one character is printed per keypress, and the machine prints the characters by making ink impressions of type elements similar to the pieces...
s. A "'miraculous machine' -- a mechanical process which could work on Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
's decision problem" (Hodges p. 98) had been suggested by G. H. Hardy
G. H. Hardy
Godfrey Harold “G. H.” Hardy FRS was a prominent English mathematician, known for his achievements in number theory and mathematical analysis....
, one of Turing's teachers. Nevertheless, "His machine had no obvious model in anything that existed in 1936, except in general terms of the new electrical industries, with their teleprinter
Teleprinter
A teleprinter is a electromechanical typewriter that can be used to communicate typed messages from point to point and point to multipoint over a variety of communication channels that range from a simple electrical connection, such as a pair of wires, to the use of radio and microwave as the...
s, television
Television
Television is a telecommunication medium for transmitting and receiving moving images that can be monochrome or colored, with accompanying sound...
'scanning', and automatic telephone exchange connections. It was his own invention." (Hodges p.109)
Davis (2000) says that Turing built a binary multiplier
Binary multiplier
A binary multiplier is an electronic circuit used in digital electronics, such as a computer, to multiply two binary numbers. It is built using binary adders....
out of electromechanical relays (p. 170). As noted in the history section of algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
punched or printed paper tape and punched paper cards were commonplace in the 1930's.
Boolos
George Boolos
George Stephen Boolos was a philosopher and a mathematical logician who taught at the Massachusetts Institute of Technology.- Life :...
and Jeffrey
Richard Jeffrey
Richard C. Jeffrey was an American philosopher, logician, and probability theorist. He was a native of Boston, Massachusetts....
(1974, 1999) note that "being in one state or another might be a matter of having one or another cog of a certain gear uppermost..." (p. 21).
Turing machine as a "poor mug" inside a box pulling the box along a rail
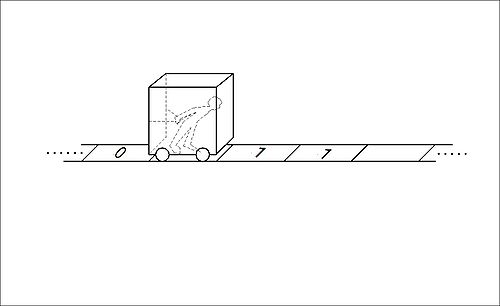
- "We are not concerned with the mechanics or the electronics of the matter. Perhaps the simplest way to picture the thing is quite crudely: Inside the box there is a man, who does all the reading and writing and erasing and moving. (The box has no bottom: the poor mug just walks along between the ties, pulling the box with him.) The man has a list of m instructions written down on a piece of paper. He is in state qi when he is carrying out instruction number i [etc.]" (Boolos and Jeffrey (1974, 1999) p.21)
This description closely follows Emil Post's "Formulation I" for a "finite combinatory process": a man, equipped with and following a "fixed unalterable set of instructions", moving left or right through "an infinite sequence of spaces or boxes" and while in a box either printing on a piece of paper a single "vertical stroke" or erasing it (Post 1936 reprinted in Undecidable p.289). Post's formulation was the first of its type to be published; it preceded Turing's by a matter of a few months.
Both descriptions-- Post's and Boolos and Jeffrey's — use simpler 4-tuples rather than 5-tuples to define the 'm-configurations' (instructions) of their processes.
A robot carries out the instructions
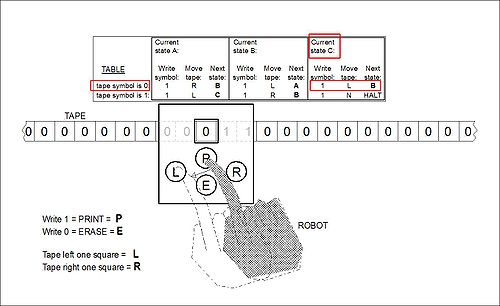
- "Let us adopt the point of view that a computer is a robot that will perform any task that can be described as a sequence of instructions" (p. 3).
Stone uses the robot to develop his notion of algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
. This in turn leads him to his description of the Turing machine and his statement:
- "The evidence seems to indicate that every algorithm for any computing device has an equivalent Turing machine algorithm ... if [Church's thesis] is true, it is certainly remarkable that Turing machines, with their extremely primitive operations, are capable of performing any computation that any other device can perform, regardless of how complex a device we choose." (p. 13)

