5-simplex	Truncated 5-simplex	Bitruncated 5-simplex
Orthogonal projections in A5 Coxeter plane

In five-dimensional geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, a truncated 5-simplex is a convex uniform 5-polytope, being a truncation

Truncation (geometry)

In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :...

 of the regular 5-simplex.

There are unique 2 degrees of truncation. Vertices of the truncation 5-simplex are located as pairs on the edge of the 5-simplex. Vertices of the bitruncation 5-simplex are located on the triangular faces of the 5-simplex.

Truncated 5-simplex

Truncated 5-simplex
Type	Uniform 5-polytope
Schläfli symbol	t0,1{3,3,3,3}
Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...	colspan=2|
4-faces	12	6 {3,3,3} 6 t{3,3,3} Truncated 5-cell In geometry, a truncated 5-cell is a uniform polychoron formed as the truncation of the regular 5-cell.There are two degrees of trunctions, including a bitruncation.- Truncated 5-cell:...
Cells	45	30 {3,3} Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... 15 t{3,3} Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :...
Faces	80	60 {3} Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... 20 {6}
Edges	75
Vertices	30
Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...	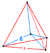Tetra.pyr
Coxeter group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...	A5 [3,3,3,3], order 720
Properties	convex Convex polytope A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...

The truncated 5-simplex has 30 vertices

Vertex (geometry)

In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...

, 75 edge

Edge (geometry)

In geometry, an edge is a one-dimensional line segment joining two adjacent zero-dimensional vertices in a polygon. Thus applied, an edge is a connector for a one-dimensional line segment and two zero-dimensional objects....

s, 80 triangular

Triangle

A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....

 faces

Face (geometry)

In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...

, 45 cells

Cell (geometry)

In geometry, a cell is a three-dimensional element that is part of a higher-dimensional object.- In polytopes :A cell is a three-dimensional polyhedron element that is part of the boundary of a higher-dimensional polytope, such as a polychoron or honeycomb For example, a cubic honeycomb is made...

 (15 tetrahedral

Tetrahedron

In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...

, and 30 truncated tetrahedron

Truncated tetrahedron

In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :...

), and 12 hypercell

Hypercell

In geometry, a hypercell is a descriptive term for an element of a polytope or tessellation, usually representing an element one dimension higher than a cell. The most generally accepted term is 4-face because it contains a 4-dimensional interior...

s (6 5-cell and 6 truncated 5-cell

Truncated 5-cell

In geometry, a truncated 5-cell is a uniform polychoron formed as the truncation of the regular 5-cell.There are two degrees of trunctions, including a bitruncation.- Truncated 5-cell:...

s).

Coordinates

The vertices of the truncated 5-simplex can be most simply constructed on a hyperplane

Hyperplane

A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...

 in 6-space as permutations of (0,0,0,0,1,2) or of (0,1,2,2,2,2). These coordinates come from facets of the truncated 6-orthoplex

Truncated 6-orthoplex

In six-dimensional geometry, a truncated 6-orthoplex is a convex uniform 6-polytope, being a truncation of the regular 6-orthoplex.There are 5 degrees of truncation for the 6-orthoplex. Vertices of the truncated 6-orthoplex are located as pairs on the edge of the 6-orthoplex. Vertices of the...

 and bitruncated 6-cube respectively.

Bitruncated 5-simplex

bitruncated 5-simplex
Type	Uniform 5-polytope
Schläfli symbol	t1,2{3,3,3,3}
Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...	colspan=2|
4-faces	12	6 t12{3,3,3} 6 t{3,3,3} Truncated 5-cell In geometry, a truncated 5-cell is a uniform polychoron formed as the truncation of the regular 5-cell.There are two degrees of trunctions, including a bitruncation.- Truncated 5-cell:...
Cells	60	45 {3,3} Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... 15 t{3,3} Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :...
Faces	140	80 {3} Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... 60 {6}
Edges	150
Vertices	60
Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
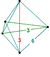Coxeter group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...	A5 [3,3,3,3], order 720
Properties	convex Convex polytope A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...

Coordinates

The vertices of the bitruncated 5-simplex can be most simply constructed on a hyperplane

Hyperplane

A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...

 in 6-space as permutations of (0,0,0,1,2,2) or of (0,0,1,2,2,2). These represent positive orthant

Orthant

In geometry, an orthant or hyperoctant is the analogue in n-dimensional Euclidean space of a quadrant in the plane or an octant in three dimensions....

 facets of the bitruncated 6-orthoplex, and the tritruncated 6-cube respectively.

Related uniform 5-polytopes

The truncated 5-simplex is one of 19 uniform polytera based on the [3,3,3,3] Coxeter group

Coxeter group

In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...

, all shown here in A₅ Coxeter plane orthographic projection

Orthographic projection

Orthographic projection is a means of representing a three-dimensional object in two dimensions. It is a form of parallel projection, where all the projection lines are orthogonal to the projection plane, resulting in every plane of the scene appearing in affine transformation on the viewing surface...

s. (Vertices are colored by projection overlap order, red, orange, yellow, green, cyan, blue, purple having progressively more vertices)

External links

• Polytopes of Various Dimensions, Jonathan Bowers
  • Truncated uniform polytera (tix), Jonathan Bowers
• Multi-dimensional Glossary