Tricritical point
Encyclopedia
In condensed matter physics
, dealing with the macroscopic physical properties of matter, a tricritical point is a point in the phase diagram
of a system at which
three-phase coexistence terminates. This definition is clearly
parallel to the definition of an ordinary critical point
as the point at which two-phase coexistence terminates.
A point of three-phase coexistence is termed a triple point
for a one-component system, since, from Gibbs' phase rule
, this condition is only achieved for a single point in the phase diagram
(F=2-3+1=0). For tricritical points to be observed, one needs a mixture with more components. It can be shown that three is the minimum number of components for which these points can appear. In this case, one may have a two-dimensional region of three-phase coexistence
(F=2-3+3=2) (thus, each point in this region corresponds to a triple point
). This region will terminate in two critical lines of phase coexistence; these two critical lines may then terminate at a single tricritical point. This point is therefore "twice critical", since it belong to two critical branches. Indeed, its critical behavior is different from critical points: the critical dimension
is lowered so the classical exponents
turn out to apply for real systems.
It seems more convenient experimentally to consider mixtures with four components for which one thermodynamic variable (usually the pressure or the volume) is kept fixed. The situation then reduces to the one described for mixtures of three components.
Historically, it was for a long time unclear whether a superconductor
undergoes a first- or a second-order phase transition.
The question was finally settled
in 1982. If the Ginzburg-Landau parameter
that distinguishes type-I
and
type-II superconductors (see also here)
is large enough, vortex fluctuations
becomes important
which drive the transition to second order
.
The tricitical point lies at
roughly
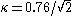, i.e., slightly below the value 
where type-I goes over into type-II superconductor.
The prediction was confirmed in 2002 by Monte Carlo computer simulations
.
Condensed matter physics
Condensed matter physics deals with the physical properties of condensed phases of matter. These properties appear when a number of atoms at the supramolecular and macromolecular scale interact strongly and adhere to each other or are otherwise highly concentrated in a system. The most familiar...
, dealing with the macroscopic physical properties of matter, a tricritical point is a point in the phase diagram
Phase diagram
A phase diagram in physical chemistry, engineering, mineralogy, and materials science is a type of chart used to show conditions at which thermodynamically distinct phases can occur at equilibrium...
of a system at which
three-phase coexistence terminates. This definition is clearly
parallel to the definition of an ordinary critical point
Critical point (thermodynamics)
In physical chemistry, thermodynamics, chemistry and condensed matter physics, a critical point, also called a critical state, specifies the conditions at which a phase boundary ceases to exist...
as the point at which two-phase coexistence terminates.
A point of three-phase coexistence is termed a triple point
Triple point
In thermodynamics, the triple point of a substance is the temperature and pressure at which the three phases of that substance coexist in thermodynamic equilibrium...
for a one-component system, since, from Gibbs' phase rule
Gibbs' phase rule
Gibbs' phase rule was proposed by Josiah Willard Gibbs in the 1870s as the equalityF\;=\;C\;-\;P\;+\;2where P is the number of phases in thermodynamic equilibrium with each other and C is the number of components. Typical phases are solids, liquids and gases. A system involving one pure chemical...
, this condition is only achieved for a single point in the phase diagram
(F=2-3+1=0). For tricritical points to be observed, one needs a mixture with more components. It can be shown that three is the minimum number of components for which these points can appear. In this case, one may have a two-dimensional region of three-phase coexistence
(F=2-3+3=2) (thus, each point in this region corresponds to a triple point
Triple point
In thermodynamics, the triple point of a substance is the temperature and pressure at which the three phases of that substance coexist in thermodynamic equilibrium...
). This region will terminate in two critical lines of phase coexistence; these two critical lines may then terminate at a single tricritical point. This point is therefore "twice critical", since it belong to two critical branches. Indeed, its critical behavior is different from critical points: the critical dimension
Critical dimension
In the renormalization group analysis of phase transitions in physics, a critical dimension is the dimensionality of space at which the character of the phase transition changes. Below the lower critical dimension there is no phase transition. Above the upper critical dimension the critical...
is lowered so the classical exponents
Landau theory
Landau theory in physics was introduced by Lev Landau in an attempt to formulate a general theory of second-order phase transitions. He was motivated to suggest that the free energy of any system should obey two conditions: that the free energy is analytic, and that it obeys the symmetry of the...
turn out to apply for real systems.
It seems more convenient experimentally to consider mixtures with four components for which one thermodynamic variable (usually the pressure or the volume) is kept fixed. The situation then reduces to the one described for mixtures of three components.
Historically, it was for a long time unclear whether a superconductor
undergoes a first- or a second-order phase transition.
The question was finally settled
in 1982. If the Ginzburg-Landau parameter
that distinguishes type-IType I superconductor
Superconductors cannot be penetrated by magnetic flux lines . This Meissner state breaks down when the applied magnetic field is too large. Superconductors can be divided into two classes according to how this breakdown occurs...
and
type-II superconductors (see also here)
is large enough, vortex fluctuations
becomes important
which drive the transition to second order
.
The tricitical point lies at
roughly
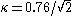, i.e., slightly below the value where type-I goes over into type-II superconductor.
The prediction was confirmed in 2002 by Monte Carlo computer simulations
Computer simulation
A computer simulation, a computer model, or a computational model is a computer program, or network of computers, that attempts to simulate an abstract model of a particular system...
.