Top tree
Encyclopedia
A Top tree is a data structure
based on a binary tree for unrooted dynamic trees
that is used mainly for various path-related operations. It allows simple divide-and-conquer algorithms. It has since been augmented to maintain dynamically various properties of a tree
such as diameter, center and median.
A Top tree
is defined for an underlying tree 
and a pair of vertices 
called as External Boundary Vertices
can be called as External Boundary Vertices, they can be thought of as Boundary Vertices of the cluster which represents the entire Top Tree.
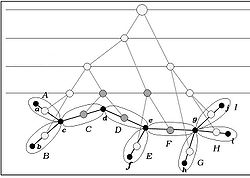
The set of Boundary Vertices of a given cluster
is denoted as 
.
With each cluster
the user may associate some meta information 
, and give methods to maintain it under the various internal operations.
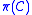contains at least one edge then 
is called a Path Cluster.
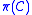does not contain any edge i.e. 
has only one Boundary Vertex then 
is called a Leaf Cluster.
A Leaf in the original Cluster is represented by a Cluster with just a single Boundary Vertex and is called a Leaf Edge Cluster.
\ 
is called an Internal Node of 
.
is called the cluster path of 
and it is denoted by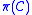 
.
and 
are Mergeable if 
is a singleton set (they have exactly one node in common) and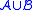 
is a Cluster.
The basic idea is to maintain a balanced Binary tree
of logarithmic height in the number of nodes in the original tree 
( i.e. in 
time) ; the Top Tree essentially represents the recursive subdivision of the original tree 
into clusters.
In general the tree
may have weight on its edges.
There is a one to one correspondence with the edges of the original tree
and the leaf nodes of the Top Tree 
and each internal node of 
represents a cluster that is formed due to the union of the clusters that are its children.
The Top Tree data structure can be initialized in
time.
Therefore the Top Tree
over (
,
) is a binary tree such that
A tree with a single node has an empty top tree, and one with just an edge is just a single node.
These trees are freely augmentable allowing the user a wide variety of flexibility and productivity without going into the details of the internal workings of the data structure, something which is also referred to as the Black Box.
Expose(v, w): Is called as a subroutine for implementing most of the path related queries on a Top Tree. It makes
and 
the External Boundary Vertices of the Top Tree and returns the new Root cluster.
Internal Operations, the sequence of which is computed in further 
time.
The next two functions are analogous to the above two and are used for base clusters.
can be represented by a Cluster Partition Tree CPT
, by replacing each cluster in the tree 
by an edge. If we use a strategy P for partitioning 
then the CPT would be CPTP
. This is done recursively till only one edge remains.
We would notice that all the nodes of the corresponding Top Tree
are uniquely mapped into the edges of this multilevel partition. There may be some edges in the multilevel partition that do not correspond to any node in the Top tree, these are the edges which represent only a single child in the level below it, i.e. a simple cluster. Only the edges that correspond to composite clusters correspond to nodes in the Top Tree 
.
A Partitioning Strategy is important while we partition the Tree
into clusters. Only a careful strategy ensures that we end up in an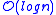 
height Multilevel Partition ( and therefore the Top Tree).
The above partitioning strategy ensures the maintenance of the Top Tree in
time.
Data structure
In computer science, a data structure is a particular way of storing and organizing data in a computer so that it can be used efficiently.Different kinds of data structures are suited to different kinds of applications, and some are highly specialized to specific tasks...
based on a binary tree for unrooted dynamic trees
Tree (data structure)
In computer science, a tree is a widely-used data structure that emulates a hierarchical tree structure with a set of linked nodes.Mathematically, it is an ordered directed tree, more specifically an arborescence: an acyclic connected graph where each node has zero or more children nodes and at...
that is used mainly for various path-related operations. It allows simple divide-and-conquer algorithms. It has since been augmented to maintain dynamically various properties of a tree
Tree (data structure)
In computer science, a tree is a widely-used data structure that emulates a hierarchical tree structure with a set of linked nodes.Mathematically, it is an ordered directed tree, more specifically an arborescence: an acyclic connected graph where each node has zero or more children nodes and at...
such as diameter, center and median.
A Top tree
is defined for an underlying tree and a pair of vertices called as External Boundary VerticesBoundary Vertex
A vertex in a connected subtree is a Boundary Vertex if it is connected to a vertex outside the subtree by an edge.External Boundary Vertices
Up to a pair of vertices in the Top Tree can be called as External Boundary Vertices, they can be thought of as Boundary Vertices of the cluster which represents the entire Top Tree.Cluster
A cluster is a connected subtree with at most two Boundary Vertices.The set of Boundary Vertices of a given cluster
is denoted as .With each cluster
the user may associate some meta information , and give methods to maintain it under the various internal operations.Path Cluster
If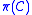 contains at least one edge then is called a Path Cluster.Leaf Cluster
If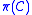 does not contain any edge i.e. has only one Boundary Vertex then is called a Leaf Cluster.Leaf Edge Cluster
A Leaf in the original Cluster is represented by a Cluster with just a single Boundary Vertex and is called a Leaf Edge Cluster.
Internal Node
A node in \ is called an Internal Node of .Cluster Path
The path between the Boundary Vertices of is called the cluster path of and it is denoted by 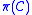.Mergeable Clusters
Two Clusters and are Mergeable if is a singleton set (they have exactly one node in common) and 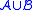is a Cluster.Introduction
Top Trees are used for maintaining a Dynamic forest (set of trees) under link and cut operations.The basic idea is to maintain a balanced Binary tree
Binary tree
In computer science, a binary tree is a tree data structure in which each node has at most two child nodes, usually distinguished as "left" and "right". Nodes with children are parent nodes, and child nodes may contain references to their parents. Outside the tree, there is often a reference to...
of logarithmic height in the number of nodes in the original tree ( i.e. in time) ; the Top Tree essentially represents the recursive subdivision of the original tree into clusters.In general the tree
may have weight on its edges.There is a one to one correspondence with the edges of the original tree
and the leaf nodes of the Top Tree and each internal node of represents a cluster that is formed due to the union of the clusters that are its children.The Top Tree data structure can be initialized in
time.Therefore the Top Tree
over (,) is a binary tree such that- The nodes of
are clusters of (
, 
); - The leaves of
are the edges of 
; - Sibling clusters are neighbours in the sense that they intersect in a single vertex, and then their parent cluster is their union.
- Root of
if the tree 
itself, with a set of at most two External Boundary Vertices.
A tree with a single node has an empty top tree, and one with just an edge is just a single node.
These trees are freely augmentable allowing the user a wide variety of flexibility and productivity without going into the details of the internal workings of the data structure, something which is also referred to as the Black Box.
Dynamic Operations
The following two are the user allowable Forest Updates.- Link(v, w): Where
and 
are nodes in different trees 
1 and 
2. It returns a single top tree representing 
v
w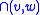
- Cut(v, w): Removes the Edge
from a tree 
with Top Tree 
, thereby turning it into two trees 
v and 
w and returning two Top Trees 
v and 
w.
Expose(v, w): Is called as a subroutine for implementing most of the path related queries on a Top Tree. It makes
and the External Boundary Vertices of the Top Tree and returns the new Root cluster.Internal Operations
The Forest updates are all carried out by a sequence of at most Internal Operations, the sequence of which is computed in further time.- Merge
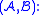Here 
and 
are Mergeable Clusters, it reutrns 
as the parent cluster of 
and 
and with boundary vertices as the boundary vertices of 
. Updates to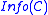 
are carried out accordingly.
- Split
: Here 
is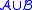 
. This deletes the cluster 
from 
methods are then called to update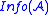 
and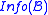 
.
The next two functions are analogous to the above two and are used for base clusters.
- Create
: Creates a cluster 
for the edge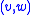 
. Sets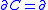 
. Methods are then called to compute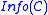 
.
- Eradicate
: 
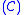is the edge cluster 
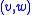. It deletes the cluster 
from the top tree. The 
is stored by calling a user defined function, as it may also happen that during a tree update, a leaf cluster may change to a path cluster and the converse.
Interesting Results and Applications
A number of interesting applications have been derived for these Top Trees some of them include- ([SLEATOR AND TARJAN 1983]). We can maintain a dynamic collection of weighted trees in
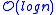time per link and cut, supporting queries about the maximum edge weight between any two vertices in O (log n) time.
- Proof outline: It involves maintaining at each node the maximum weight (max_wt) on its cluster path, if it is a point cluster then max_wt(
) is initialsed as 
. When a cluster is a union of two clusters then it is the maximum value of the two merged clusters. If we have to find the max wt between 
and 
then we do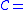 
Expose
, and report max_wt
.
- Proof outline: It involves maintaining at each node the maximum weight (max_wt) on its cluster path, if it is a point cluster then max_wt(
- ([SLEATOR AND TARJAN 1983]). In the scenario of the above application we can also add a common weight
to all edges on a given path 
· · ·
in 
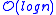time.
- Proof outline: We introduce a weight called extra(
) to be added to all the edges in 
. Which is maintained appropriately ; split(
) requires that, for each path child 
of 
, we set max_wt(A) := max_wt(
) + extra(
) and extra(
) := extra(
) + extra(
). For 
:= join(
, 
), we set max_wt(
) := max {max_wt(
), max_wt(
)} and extra(
) := 0. Finally, to find the maximum weight on the path 
· · ·
, we set 
:= Expose
and return max_wt(
).
- Proof outline: We introduce a weight called extra(
- ([GOLDBERG ET AL. 1991]). We can ask for the maximum weight in the underlying tree containing a given vertex
in 
time.
- Proof outline: This requires maintaining additional information about the maximum weight non cluster path edge in a cluster under the Merge and Split operations.
- The distance between two vertices
and 
can be found in 
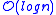time as length(Expose
).
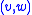- Proof outline:We will maintain the length length(
) of the cluster path. The length is maintained as the maximum weight except that, if 
is created by a join(Merge), length(
) is the sum of lengths stored with its path children.
- Proof outline:We will maintain the length length(
- Queries regarding diameter of a tree and its subsequent maintenance takes
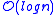time.
- The Center and Median can me maintained under Link(Merge) and Cut(Split) operations in
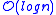time.
Implementation
Top Trees have been implemented in a variety of ways, some of them include implementation using a Multilevel Partition (Top-trees and dynamic graph algorithms Jacob Holm and Kristian de Lichtenberg. Technical Report), and even by using Sleator-Tarjan s-t trees, Fredericksons Topology Trees (Alstrup et al. Maintaining Information in Fully Dynamic Trees with Top Trees).Using Multilevel Partitioning
Any partitioning of clusters of a tree can be represented by a Cluster Partition Tree CPT, by replacing each cluster in the tree by an edge. If we use a strategy P for partitioning then the CPT would be CPTP. This is done recursively till only one edge remains.We would notice that all the nodes of the corresponding Top Tree
are uniquely mapped into the edges of this multilevel partition. There may be some edges in the multilevel partition that do not correspond to any node in the Top tree, these are the edges which represent only a single child in the level below it, i.e. a simple cluster. Only the edges that correspond to composite clusters correspond to nodes in the Top Tree .A Partitioning Strategy is important while we partition the Tree
into clusters. Only a careful strategy ensures that we end up in an 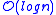height Multilevel Partition ( and therefore the Top Tree).
- The number of edges in subsequent levels should decrease by a constant factor.
- If a lower level is changed by an update then we should be able to update the one immediately above it using at most a constant number of insertions and deletions.
The above partitioning strategy ensures the maintenance of the Top Tree in
time.