Tolman length
Encyclopedia
The Tolman length 
measures the extent by which the surface tension
of a small liquid drop deviates from its planar value. It is conveniently defined in terms of an expansion in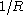
, with 
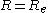the equimolar radius of the liquid drop, of the pressure difference across the droplet's surface:
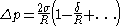(1)
In this expression,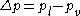
is the pressure difference between the (bulk) pressure of the liquid inside and the pressure of the vapour outside, and 
is the surface tension
of the planar interface, i.e. the interface with zero curvature
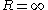. The Tolman length 
is thus defined as the leading order correction in an expansion in 
.
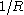Another way to define the tolman length is to consider the radius dependence of the surface tension,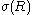
. To leading order in 
one has:
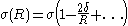(2)
Here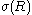
denotes the surface tension (or (excess) surface free energy) of a liquid drop with radius R, whereas 
denotes its value in the planar limit.
In both definitions (1) and (2) the Tolman length is defined as a coefficient in an expansion in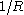
and therefore does not depend on R.
Furthermore, the Tolman length can be related to the radius of spontaneous curvature when one compares the free energy
method of Helfrich with the method of Tolman:
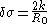
Any result for the Tolman length therefore gives information about the radius of spontaneous curvature,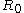
. If the Tolman length is known to be positive (with k > 0) the interface tends to curve towards the liquid phase, whereas a negative Tolman length implies a negative 
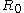and a preferred curvature towards the vapour phase.
Apart from being related to the radius of spontaneous curvature, the Tolman length can also be linked to the surface of tension. The surface of tension, positioned at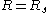
, is defined as the surface for which the Laplace equation holds exactly for all droplet radii:
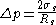
where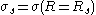
is the surface tension at the surface of tension. Using the Gibbs adsorption equation, Tolman himself showed that the Tolman length can be expressed in terms of the adsorbed amount at the surface of tension at coexistence
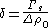
where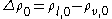
; the subscript zero to the density denotes the value at two-phase coexistence. It can be shown that the difference between the location of the surface of tension and of the equimolar dividing surface proposed by Gibbs yields the value of the Tolman length:
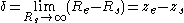
where the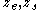
denote the locations of the corresponding surfaces making the magnitude of the Tolman length in the order of nanometers.
measures the extent by which the surface tensionSurface tension
Surface tension is a property of the surface of a liquid that allows it to resist an external force. It is revealed, for example, in floating of some objects on the surface of water, even though they are denser than water, and in the ability of some insects to run on the water surface...
of a small liquid drop deviates from its planar value. It is conveniently defined in terms of an expansion in
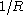, with 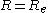the equimolar radius of the liquid drop, of the pressure difference across the droplet's surface: 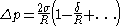(1)In this expression,
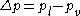is the pressure difference between the (bulk) pressure of the liquid inside and the pressure of the vapour outside, and is the surface tensionSurface tension
Surface tension is a property of the surface of a liquid that allows it to resist an external force. It is revealed, for example, in floating of some objects on the surface of water, even though they are denser than water, and in the ability of some insects to run on the water surface...
of the planar interface, i.e. the interface with zero curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
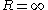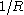. The Tolman length is thus defined as the leading order correction in an expansion in .Another way to define the tolman length is to consider the radius dependence of the surface tension,
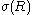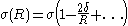. To leading order in one has: (2)Here
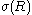denotes the surface tension (or (excess) surface free energy) of a liquid drop with radius R, whereas denotes its value in the planar limit.In both definitions (1) and (2) the Tolman length is defined as a coefficient in an expansion in
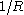and therefore does not depend on R.Furthermore, the Tolman length can be related to the radius of spontaneous curvature when one compares the free energy
Thermodynamic free energy
The thermodynamic free energy is the amount of work that a thermodynamic system can perform. The concept is useful in the thermodynamics of chemical or thermal processes in engineering and science. The free energy is the internal energy of a system less the amount of energy that cannot be used to...
method of Helfrich with the method of Tolman:
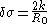
Any result for the Tolman length therefore gives information about the radius of spontaneous curvature,
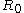. If the Tolman length is known to be positive (with k > 0) the interface tends to curve towards the liquid phase, whereas a negative Tolman length implies a negative 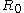and a preferred curvature towards the vapour phase.Apart from being related to the radius of spontaneous curvature, the Tolman length can also be linked to the surface of tension. The surface of tension, positioned at
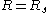, is defined as the surface for which the Laplace equation holds exactly for all droplet radii: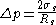 where
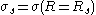is the surface tension at the surface of tension. Using the Gibbs adsorption equation, Tolman himself showed that the Tolman length can be expressed in terms of the adsorbed amount at the surface of tension at coexistence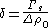 where
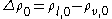; the subscript zero to the density denotes the value at two-phase coexistence. It can be shown that the difference between the location of the surface of tension and of the equimolar dividing surface proposed by Gibbs yields the value of the Tolman length: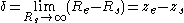 where the
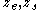denote the locations of the corresponding surfaces making the magnitude of the Tolman length in the order of nanometers.