Timsort
Encyclopedia
Timsort is a hybrid sorting algorithm
, derived from merge sort
and insertion sort
, designed to perform well on many kinds of real-world data. It was invented by Tim Peters in 2002 for use in the Python programming language
. The algorithm
is designed to find subsets of the data which are already ordered and use them to sort the data more efficiently. This is done by merging an identified subset, called a run, with the existing runs until certain criteria are fulfilled.
Timsort has been Python's standard sorting algorithm since version 2.3. It is now also used to sort arrays in Java SE 7, and on the Android platform.
The size of the run is checked against the minimum run size. The minimum run size (minrun) depends on the size of the array
. For an array of fewer than 64 elements, the minrun is the size of the array, making Timsort essentially an insertion sort. For larger arrays, a number, referred to as minrun, is chosen from the range 32 to 65, such that the size of the array divided by the minimum run size is equal to, or slightly smaller than, a power of two. The final algorithm for this simply takes the most significant six bits of the size of the array, adds one if any of the remaining bits are set, and uses that as the minrun. This algorithm works for all the cases including the one in which the size of the array is smaller than 64.
Thus, merging is always done on two consecutive runs. For this, the three top-most runs in the stack which are unsorted are considered. If, say, X, Y, Z represent the lengths of the three uppermost runs in the stack, the algorithm merges the runs so that ultimately the following two rules are satisfied:
For example, if the first of the two rules is not satisfied by the current run status, that is, if X < Y + Z, then, Y is merged with the smaller of X and Z. The merging continues until both the rules are satisfied. Then the algorithm goes on to determine the next run.
The rules above aim at maintaining run lengths as close to each other as possible to ensure balanced merges, which are more efficient. At the same time only a small number of runs may be remembered, as the stack is of a specific size. The algorithm also tries to exploit the fresh occurrence of the runs to be merged, in cache memory
. Thus a compromise is attained between delaying merging, and exploiting fresh occurrence in cache memory.
A simple merge algorithm is then run left to right or right to left depending on which run is smaller, on the temporary memory and original memory of the larger run, the final sorted run being stored in the original memory of the two initial runs. In order to make this more efficient, Timsort searches for appropriate positions for starting element of one array in the other using an adaption of binary search. Say, for example, two runs A and B are to be merged, with A as the smaller run. In that case a binary search is conducted in order to find at what position in A the first element of B will fit. Note that in this situation A and B are already sorted individually. Therefore, when such an appropriate position is found, the algorithm can ignore elements before that position in A while inserting (after comparing) elements of B. Similarly, the algorithm also looks for what position the last element of A can take in B. The elements in B after this position can also be ignored for the sorting. This preliminary searching may not prove efficient in the case of random data, however it is found to be highly efficient in other situations and is hence included.
When in galloping mode, the algorithm searches for the first element of one array in the other. This is done by comparing that first element (initial element) with the zeroth element of the other array, then the first, the third and so on, that is (2k - 1)th element, so as to get a range of elements between which the initial element will lie. This provides a shorter range to conduct binary search on, thus increasing efficiency. Galloping proves to be more efficient except in cases with especially long runs and random data usually has shorter runs. Also, in cases where galloping is found to be less efficient as compared to binary search
, galloping mode is exited from.
However it is found that galloping is not always efficient. One reason is due to excessive function calls. Function calls are expensive and thus when they are large in number, they hamper program efficiency. Further there are cases where galloping mode requires more number of comparisons than a simple linear search
(one at a time search). While for the first few cases both modes may require the same number of comparisons, over time galloping mode requires 33% more comparisons than linear search to arrive at the same results. Moreover all comparisons in galloping mode are done by function calls.
Also, it is seen that galloping is beneficial only when the initial element is not one of the first seven elements of the other run. This also results in MIN_GALLOP being set to 7. To avoid the drawbacks of galloping mode, the merging functions adjust the value of min-gallop. If the element is from the array currently under consideration (that is, the array which has been returning the elements consecutively for a while), the value of min-gallop is reduced by one. Otherwise, the value is incremented by one, thus discouraging entry back to galloping mode. When this is done, in the case of random data, the value of min-gallop becomes so large, that the entry back to galloping mode never takes place.
In the case where merge-hi is used (that is, merging is done right-to-left), galloping needs to start from the right end of the data, that is the last element. Galloping from the beginning also gives the required results, but makes more comparisons than required.
Thus, the algorithm for galloping includes the use of a variable which gives the index at which galloping should begin. Thus the algorithm can enter galloping mode at any index and continue thereon as mentioned above, as in, it will check at the next index which is offset by 1, 3, 7,...., (2k - 1).. and so on from the current index. In the case of merge-hi, the offsets to the index will be -1, -3, -7,....
, no comparison sort
can perform better than
comparisons in the average case. On real-world data, Timsort often requires far fewer than 
comparisons, because it takes advantage of the fact that sublists of the data may already be in order. In case of random data, there are no partially ordered subarrays to take advantage of. In this case, timsort approches the theoretical limit of lg(n!), which is in 
.
The following table compares the time complexity of timsort with other comparison sorts.
The following table provides a comparison of the space complexities of the various sorting techniques. Note that for mergesort, the worst case space complexity is O(n).
Sorting algorithm
In computer science, a sorting algorithm is an algorithm that puts elements of a list in a certain order. The most-used orders are numerical order and lexicographical order...
, derived from merge sort
Merge sort
Merge sort is an O comparison-based sorting algorithm. Most implementations produce a stable sort, meaning that the implementation preserves the input order of equal elements in the sorted output. It is a divide and conquer algorithm...
and insertion sort
Insertion sort
Insertion sort is a simple sorting algorithm: a comparison sort in which the sorted array is built one entry at a time. It is much less efficient on large lists than more advanced algorithms such as quicksort, heapsort, or merge sort...
, designed to perform well on many kinds of real-world data. It was invented by Tim Peters in 2002 for use in the Python programming language
Python (programming language)
Python is a general-purpose, high-level programming language whose design philosophy emphasizes code readability. Python claims to "[combine] remarkable power with very clear syntax", and its standard library is large and comprehensive...
. The algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
is designed to find subsets of the data which are already ordered and use them to sort the data more efficiently. This is done by merging an identified subset, called a run, with the existing runs until certain criteria are fulfilled.
Timsort has been Python's standard sorting algorithm since version 2.3. It is now also used to sort arrays in Java SE 7, and on the Android platform.
Operation
Timsort is designed to take advantage of partial ordering that already exists in most real-world data. Timsort operates by finding runs in the data. A run is a sub-array, at least two elements long, which is either non-descending (each element is equal to or higher than its predecessor) or strictly descending (each element is lower than its predecessor). If it is descending, it must be strictly descending, since these runs are later reversed by a simple swap of elements from both ends converging in the middle. This method is stable if the elements are present in a strictly descending order. After obtaining such a run in the given array, timsort processes it; and then continues its search for the next run.Minrun
A natural run is a sub-array which is already ordered. Natural runs in real-time data may be of varied lengths. Timsort efficiently chooses a particular type of sorting technique depending on the length of the run (for example if the run length is smaller than a certain value, insertion sort is used). Thus it is termed as an adaptive sort.The size of the run is checked against the minimum run size. The minimum run size (minrun) depends on the size of the array
Array
In computer science, an array data structure or simply array is a data structure consisting of a collection of elements , each identified by at least one index...
. For an array of fewer than 64 elements, the minrun is the size of the array, making Timsort essentially an insertion sort. For larger arrays, a number, referred to as minrun, is chosen from the range 32 to 65, such that the size of the array divided by the minimum run size is equal to, or slightly smaller than, a power of two. The final algorithm for this simply takes the most significant six bits of the size of the array, adds one if any of the remaining bits are set, and uses that as the minrun. This algorithm works for all the cases including the one in which the size of the array is smaller than 64.
Insertion Sort
When an array is random, a natural run is most likely to contain less than minrun elements. In this case, an appropriate number of succeeding elements are considered and insertion sort is used on them, thus increasing the size of the run to minrun size. Thus, most runs in a random array are or become minrun in length. This results in balanced merges, which provides an efficient way to proceed; it also results in a reasonable number of function calls in the implementation of the sort.Merge Memory
Once run lengths are optimized, the runs are merged. The principle of Timsort implies that it will be merged by a specific technique which will ensure the highest efficiency. When a run is found, the algorithm pushes its base address and length on a stack. A function is then called which determines whether it should be merged with previous runs. Timsort does not merge non-consecutive runs because doing this would cause the element common to all three runs to become out of order with respect to the middle run.Thus, merging is always done on two consecutive runs. For this, the three top-most runs in the stack which are unsorted are considered. If, say, X, Y, Z represent the lengths of the three uppermost runs in the stack, the algorithm merges the runs so that ultimately the following two rules are satisfied:
- X > Y + Z
- Y > Z
For example, if the first of the two rules is not satisfied by the current run status, that is, if X < Y + Z, then, Y is merged with the smaller of X and Z. The merging continues until both the rules are satisfied. Then the algorithm goes on to determine the next run.
The rules above aim at maintaining run lengths as close to each other as possible to ensure balanced merges, which are more efficient. At the same time only a small number of runs may be remembered, as the stack is of a specific size. The algorithm also tries to exploit the fresh occurrence of the runs to be merged, in cache memory
CPU cache
A CPU cache is a cache used by the central processing unit of a computer to reduce the average time to access memory. The cache is a smaller, faster memory which stores copies of the data from the most frequently used main memory locations...
. Thus a compromise is attained between delaying merging, and exploiting fresh occurrence in cache memory.
Merging Procedure
Merging two adjacent runs is done with the help of temporary memory. The temporary memory is of the size of the minimum of the two runs. The algorithm copies the smaller of the two runs into this temporary memory and then uses the original memory (of the smaller run) and the memory of the other run to store the final run after sorting.A simple merge algorithm is then run left to right or right to left depending on which run is smaller, on the temporary memory and original memory of the larger run, the final sorted run being stored in the original memory of the two initial runs. In order to make this more efficient, Timsort searches for appropriate positions for starting element of one array in the other using an adaption of binary search. Say, for example, two runs A and B are to be merged, with A as the smaller run. In that case a binary search is conducted in order to find at what position in A the first element of B will fit. Note that in this situation A and B are already sorted individually. Therefore, when such an appropriate position is found, the algorithm can ignore elements before that position in A while inserting (after comparing) elements of B. Similarly, the algorithm also looks for what position the last element of A can take in B. The elements in B after this position can also be ignored for the sorting. This preliminary searching may not prove efficient in the case of random data, however it is found to be highly efficient in other situations and is hence included.
Galloping Mode
Generally the merge occurs in what is called the ‘one pair at a time’ mode, where respective elements of both runs are compared. In the case where function merge_lo is invoked, that is, when the algorithm merges left-to-right, the smaller of the two is brought to a merge area. A count of the number of times the final element appears from a given run is recorded. When this value reaches a certain value, MIN_GALLOP, the merge switches to what is called the ‘galloping mode’. In this mode we use the a previously mentioned adaptation of binary search to identify where the first element of the smaller array must be placed in the larger array and vice-verse . Thus the entire set of elements, in one array, occurring before this location can be moved all together to the merge area and the other way round. This is possible as we have both the runs to be merged, as ordered individually. The galloping mode is entered only when it is the most optimum method to merge; this is decided by the value of min-gallop. Min-gallop is a variable initialized to MIN_GALLOP. However the functions merge-lo and merge-hi increment the value of the variable, if galloping is not efficient, and decrement it if it is. The moment too many consecutive elements come from different runs, galloping mode is exited.When in galloping mode, the algorithm searches for the first element of one array in the other. This is done by comparing that first element (initial element) with the zeroth element of the other array, then the first, the third and so on, that is (2k - 1)th element, so as to get a range of elements between which the initial element will lie. This provides a shorter range to conduct binary search on, thus increasing efficiency. Galloping proves to be more efficient except in cases with especially long runs and random data usually has shorter runs. Also, in cases where galloping is found to be less efficient as compared to binary search
Binary search algorithm
In computer science, a binary search or half-interval search algorithm finds the position of a specified value within a sorted array. At each stage, the algorithm compares the input key value with the key value of the middle element of the array. If the keys match, then a matching element has been...
, galloping mode is exited from.
However it is found that galloping is not always efficient. One reason is due to excessive function calls. Function calls are expensive and thus when they are large in number, they hamper program efficiency. Further there are cases where galloping mode requires more number of comparisons than a simple linear search
Linear search
In computer science, linear search or sequential search is a method for finding a particular value in a list, that consists of checking every one of its elements, one at a time and in sequence, until the desired one is found....
(one at a time search). While for the first few cases both modes may require the same number of comparisons, over time galloping mode requires 33% more comparisons than linear search to arrive at the same results. Moreover all comparisons in galloping mode are done by function calls.
Also, it is seen that galloping is beneficial only when the initial element is not one of the first seven elements of the other run. This also results in MIN_GALLOP being set to 7. To avoid the drawbacks of galloping mode, the merging functions adjust the value of min-gallop. If the element is from the array currently under consideration (that is, the array which has been returning the elements consecutively for a while), the value of min-gallop is reduced by one. Otherwise, the value is incremented by one, thus discouraging entry back to galloping mode. When this is done, in the case of random data, the value of min-gallop becomes so large, that the entry back to galloping mode never takes place.
In the case where merge-hi is used (that is, merging is done right-to-left), galloping needs to start from the right end of the data, that is the last element. Galloping from the beginning also gives the required results, but makes more comparisons than required.
Thus, the algorithm for galloping includes the use of a variable which gives the index at which galloping should begin. Thus the algorithm can enter galloping mode at any index and continue thereon as mentioned above, as in, it will check at the next index which is offset by 1, 3, 7,...., (2k - 1).. and so on from the current index. In the case of merge-hi, the offsets to the index will be -1, -3, -7,....
Performance
According to information theoryInformation theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
, no comparison sort
Comparison sort
A comparison sort is a type of sorting algorithm that only reads the list elements through a single abstract comparison operation that determines which of two elements should occur first in the final sorted list...
can perform better than
comparisons in the average case. On real-world data, Timsort often requires far fewer than comparisons, because it takes advantage of the fact that sublists of the data may already be in order. In case of random data, there are no partially ordered subarrays to take advantage of. In this case, timsort approches the theoretical limit of lg(n!), which is in . The following table compares the time complexity of timsort with other comparison sorts.
| Timsort | Merge Sort | Quick Sort | Insertion Sort | Selection Sort | |
|---|---|---|---|---|---|
| Best Case |  |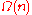
 |
 |
 |
 |
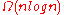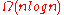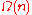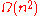| Average Case |  |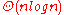
 |
 |
 |
 |
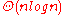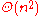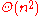| Worst Case |  |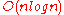
 |
 |
 |
 |
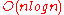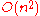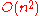The following table provides a comparison of the space complexities of the various sorting techniques. Note that for mergesort, the worst case space complexity is O(n).
| Timsort | Merge Sort Merge sort Merge sort is an O comparison-based sorting algorithm. Most implementations produce a stable sort, meaning that the implementation preserves the input order of equal elements in the sorted output. It is a divide and conquer algorithm... |
Quick Sort | Insertion Sort Insertion sort Insertion sort is a simple sorting algorithm: a comparison sort in which the sorted array is built one entry at a time. It is much less efficient on large lists than more advanced algorithms such as quicksort, heapsort, or merge sort... |
Selection Sort Selection sort Selection sort is a sorting algorithm, specifically an in-place comparison sort. It has O time complexity, making it inefficient on large lists, and generally performs worse than the similar insertion sort... |
|
|---|---|---|---|---|---|
| Space Complexity | n | n | log n | 1 | 1 |
External links
- Visualising Timsort - the source for the image on this page.
- Python's listobject.c - the CC (programming language)C is a general-purpose computer programming language developed between 1969 and 1973 by Dennis Ritchie at the Bell Telephone Laboratories for use with the Unix operating system....
implementation of timsort for CPythonCPythonCPython is the default, most-widely used implementation of the Python programming language. It is written in C. In addition to CPython, there are two other production-quality Python implementations: Jython, written in Java, and IronPython, which is written for the Common Language Runtime. There...
. - OpenJDK's TimSort.java - the Java implementation of timsort.