Three subgroups lemma
Encyclopedia
In mathematics
, more specifically group theory
, the three subgroups lemma is a result concerning commutator
s. It is a consequence of the Hall–Witt identity.
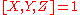and 
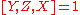
Then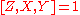
.
More generally, if
, then if 
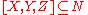and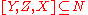 
, then 
.
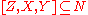If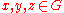
, then
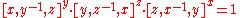
Proof of the Three subgroups lemma
Let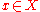
, 
, and 
. Then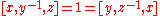 
, and by the Hall–Witt identity above, it follows that 
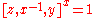and so 
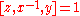. Therefore, 
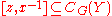for all 
and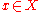 
. Since these elements generate 
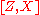, we conclude that 
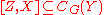and hence 
.
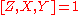Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, more specifically group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, the three subgroups lemma is a result concerning commutator
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
s. It is a consequence of the Hall–Witt identity.
Notation
In that which follows, the following notation will be employed:- If H and K are subgroups of a group G, the commutatorCommutatorIn mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
of H and K will be denoted by [H,K]; if L is a third subgroup, the convention that [H,K,L] = i>H,K],L] will be followed. - If x and y are elements of a group G, the conjugate of x by y will be denoted by
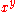. - If H is a subgroup of a group G, then the centralizerCentralizer and normalizerIn group theory, the centralizer and normalizer of a subset S of a group G are subgroups of G which have a restricted action on the elements of S and S as a whole, respectively...
of H in G will be denoted by CG(H).
Statement
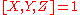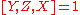
Let X, Y and Z be subgroups of a group G, and assume and Then
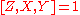.More generally, if
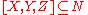, then if and 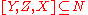, then 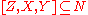.Proof and the Hall–Witt identity
Hall–Witt identityIf
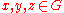, then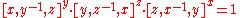Proof of the Three subgroups lemma
Let
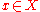, , and . Then 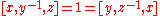, and by the Hall–Witt identity above, it follows that 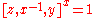and so 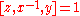. Therefore, 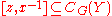for all and 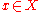. Since these elements generate 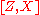, we conclude that 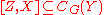and hence .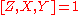