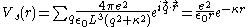Thomas-Fermi screening
Encyclopedia
The mobile charge carriers damp down the electric fields in materials. This is called Electric field screening
.
Thomas-Fermi screening is one of many approximation methods for describing the screening.
Thomas-Fermi screening assumes that the total potential varies very slowly, the chemical potential of the system is constant and the temperature is very low.
|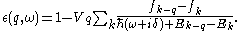
|}
Here,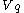 is
is  and
and 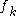 is the carrier distribution function which is the Fermi-Dirac distribution function(see also Fermi–Dirac statistics) for electrons in thermodynamic equilibrium.
is the carrier distribution function which is the Fermi-Dirac distribution function(see also Fermi–Dirac statistics) for electrons in thermodynamic equilibrium.
However this Lindhard formula is valid also for nonequilibrium distribution functions.
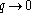 ).
).
For denominator of Lindhard formula,
and for numerator of Lindhard formula,
Inserting these to Lindhard formula and taking limit, we obtain
limit, we obtain
Electric field screening
Screening is the damping of electric fields caused by the presence of mobile charge carriers. It is an important part of the behavior of charge-carrying fluids, such as ionized gases and conduction electrons in semiconductors and metals....
.
Thomas-Fermi screening is one of many approximation methods for describing the screening.
Thomas-Fermi screening assumes that the total potential varies very slowly, the chemical potential of the system is constant and the temperature is very low.
Lindhard formula
Lindhard formula for the longitudinal dielectric function is given by-
- {|cellpadding="2" style="border:2px solid #ccccff"
|
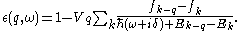
|}
Here,
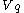 is
is  and
and 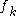 is the carrier distribution function which is the Fermi-Dirac distribution function(see also Fermi–Dirac statistics) for electrons in thermodynamic equilibrium.
is the carrier distribution function which is the Fermi-Dirac distribution function(see also Fermi–Dirac statistics) for electrons in thermodynamic equilibrium.However this Lindhard formula is valid also for nonequilibrium distribution functions.
Analysis of the Lindhard formula
For understanding the Lindhard formula, let's consider some limiting cases in 3 dimensions and 2 dimensions. 1 dimension case is also considered in other way.Long Wave-length Limit
First, consider the long wave-length limit (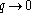 ).
).For denominator of Lindhard formula,
-
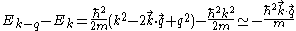 ,
,
and for numerator of Lindhard formula,
-
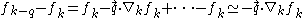 .
.
Inserting these to Lindhard formula and taking
 limit, we obtain
limit, we obtain-
 ,
,
where we used ,
, 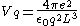 and
and 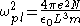 .
.
This result is same as the classical dielectric function.
Static Limit
Second, consider the static limit ( ).
).
The Lindhard formula becomes-
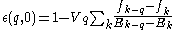 .
.
Inserting above equalities for denominator and numerator to this, we obtain
-
 .
.
Assuming a thermal equilibrium Fermi-Dirac carrier distribution, we get-
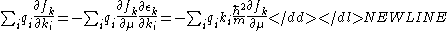
here, we used and
and 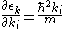 .
.
Therefore,-
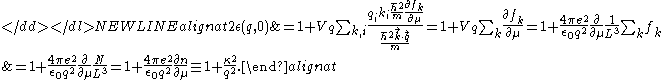
 is 3D screening wave number(3D inverse screening length) defined as
is 3D screening wave number(3D inverse screening length) defined as
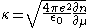 .
.
Then, the 3D statically screened Coulomb potential is given by-
 .
.
And Fourier transformation of this result gives
as we call it Yukawa potential.
For a degenerating gas(T=0), Fermi energyFermi energyThe Fermi energy is a concept in quantum mechanics usually referring to the energy of the highest occupied quantum state in a system of fermions at absolute zero temperature....
is given by-
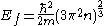 ,
,
So the density is-
 .
.
At T=0,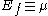 , so
, so 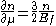 .
.
Inserting this to above 3D screening wave number equation, we get
-
- {|cellpadding="2" style="border:2px solid #ccccff"
|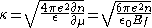 .
.
|}
This is 3D Thomas-Fermi screening wave number.
For reference, Debye-Hückel screeningDebye lengthIn plasma physics, the Debye length , named after the Dutch physicist and physical chemist Peter Debye, is the scale over which mobile charge carriers screen out electric fields in plasmas and other conductors. In other words, the Debye length is the distance over which significant charge...
describes the nondegenerate limit case.
The result is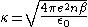 , 3D Debye-Hückel screening wave number.
, 3D Debye-Hückel screening wave number.
Long Wave-length Limit
First, consider the long wave-length limit ( ).
).
For denominator of Lindhard formula,
-
 ,
,
and for numerator of Lindhard formula,
-
 .
.
Inserting these to Lindhard formula and taking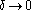 limit, we obtain
limit, we obtain
-
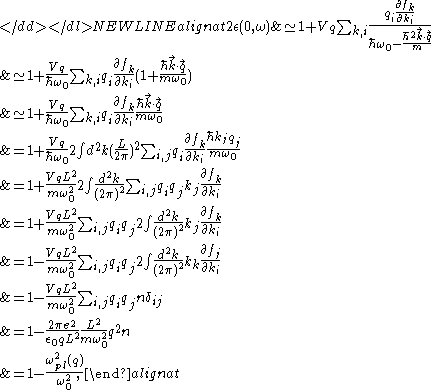
where we used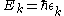 ,
, 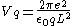 and
and  .
.
Static Limit
Second, consider the static limit (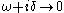 ).
).
The Lindhard formula becomes-
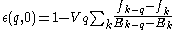 .
.
Inserting above equalities for denominator and numerator to this, we obtain
-
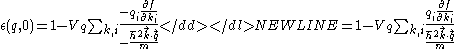 .
.
Assuming a thermal equilibrium Fermi-Dirac carrier distribution, we get-

here, we used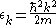 and
and 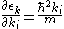 .
.
Therefore,-
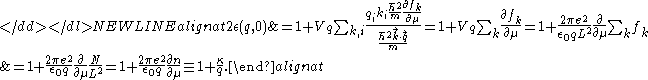
 is 2D screening wave number(2D inverse screening length) defined as
is 2D screening wave number(2D inverse screening length) defined as
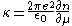 .
.
Then, the 2D statically screened Coulomb potential is given by-
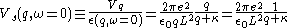 .
.
It is known that the chemical potential of the 2 dimensional Fermi gas is given by
-
 ,
,
and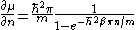 .
.
So, the 2D screening wave number is-
- {|cellpadding="2" style="border:2px solid #ccccff"
|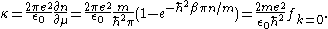
|}
Note that this result is independent of n.
One Dimension
This time, let's consider some generalized case for lowering the dimension.
The lower the dimensions is, the weaker the screening effect is.
In lower dimension, some of the field lines pass through the barrier material wherein the screening has no effect.
For 1 dimensional case, we can guess that the screening effects only on the field lines which are very close to the wire axis.
Experiment
In real experiment, we should also take the 3D bulk screening effect into account even though we deal with 1D case like the single filament.
D. Davis applied the Thomas-Fermi screening to an electron gas confined to a filament and a coaxial cylinder.
For K2Pt(CN)4Cl0.32·2.6H20, it was found that the potential within the region between the filament and cylinder varies as
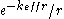 and its effective screening length is about 10 times that of metallic platinumPlatinumPlatinum is a chemical element with the chemical symbol Pt and an atomic number of 78. Its name is derived from the Spanish term platina del Pinto, which is literally translated into "little silver of the Pinto River." It is a dense, malleable, ductile, precious, gray-white transition metal...
and its effective screening length is about 10 times that of metallic platinumPlatinumPlatinum is a chemical element with the chemical symbol Pt and an atomic number of 78. Its name is derived from the Spanish term platina del Pinto, which is literally translated into "little silver of the Pinto River." It is a dense, malleable, ductile, precious, gray-white transition metal...
. -
-
-
-
-
-
-
-