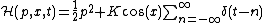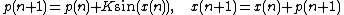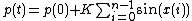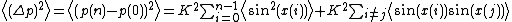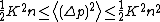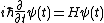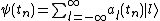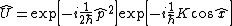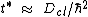The Kicked Rotator
Encyclopedia
The kicked rotator, also spelled as kicked rotor, is a prototype model for chaos
and quantum chaos
studies. It describes a particle that is constrained to move on a ring (equivalently: a rotating stick). The particle is kicked periodically by an homogeneous field (equivalently: the gravitation is switched on periodically in short pulses). The model is described by the Hamiltonian
Where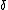 is the Dirac delta function,
is the Dirac delta function,  is the angular position (for example, on a ring), taken modulo
is the angular position (for example, on a ring), taken modulo 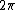 ,
, 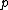 is the momentum, and
is the momentum, and 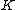 is the kicking strength. Its dynamics are described by the standard map
is the kicking strength. Its dynamics are described by the standard map
With the caveat that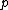 is not periodic, as it is in the standard map. See more details and references on the standard map here, or better in the associated Scholarpedia entry.
is not periodic, as it is in the standard map. See more details and references on the standard map here, or better in the associated Scholarpedia entry.
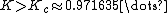 , the system is chaotic and has a positive Maximal Lyapunov exponent (MLE).
, the system is chaotic and has a positive Maximal Lyapunov exponent (MLE).
The averaged diffusion of the momentum-squared is a useful parameter in characterizing the delocalization of nearby trajectories. The inductive result of the standard map yields the following equation for momentum
The diffusion can then be calculated by squaring the difference in momentum after the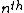 kick and the initial momentum, and then averaging, yielding
kick and the initial momentum, and then averaging, yielding
In the chaotic domain, the momenta at different time points may be anywhere from entirely uncorrelated to highly correlated. If they are assumed uncorrelated due to the quasi-random behaviour, the sum involving the cross-terms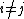 is neglected. In this limit, since the first term is a sum of
is neglected. In this limit, since the first term is a sum of  terms all equalling
terms all equalling 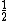 , the momentum diffusion becomes
, the momentum diffusion becomes 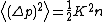 . However, if the momenta at different time points are assumed highly correlated, the sum involving the cross-terms is not neglected, and so it contributes more terms equalling
. However, if the momenta at different time points are assumed highly correlated, the sum involving the cross-terms is not neglected, and so it contributes more terms equalling 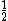 . Altogether, there are
. Altogether, there are 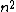 terms to sum, all of the form
terms to sum, all of the form 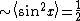 . This gives an upper bound on the momentum diffusion of
. This gives an upper bound on the momentum diffusion of 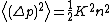 . Therefore, in the chaotic domain, the momentum diffusion is between
. Therefore, in the chaotic domain, the momentum diffusion is between
That is, the momentum diffusion in the chaotic domain has somewhere between a linear and a quadratic dependence on the number of kicks. An exact expression for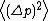 can be obtained in principle by calculating the sums explicitly for an ensemble of trajectories.
can be obtained in principle by calculating the sums explicitly for an ensemble of trajectories.
 to give (in dimensionless form)
to give (in dimensionless form)
The wavefunction can then be solved for using Schrödinger's equation
where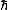 is here scaled according to the period between kicks,
is here scaled according to the period between kicks, 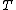 , and the wave-vector of the driving potential,
, and the wave-vector of the driving potential, 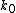 , as
, as
The wavefunction at the kick can be expanded in terms of the momentum eigenstates,
kick can be expanded in terms of the momentum eigenstates, 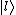 , as
, as
It can be shown that the coefficients are given recursively by
Where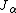 is a Bessel function of order
is a Bessel function of order  .
.
Given some set of initial conditions, it is relatively straightforward to numerically solve the recursive equation above for all time, and substitute the calculated coefficients back into the momentum eigenstate decomposition to find the total wavefunction. Squaring this gives the time evolution of the probability distribution, thus providing a complete a quantum mechanical description.
Another way to calculate the time evolution is to iteratively apply the unitary operator
It has been discovered that the classical diffusion is suppressed, and later it has been understood that this is a manifestation of a quantum dynamical localization effect that parallels Anderson localization
. There is a general argument that leads to the following estimate for the breaktime of the diffusive behavior
Where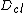 is the classical diffusion coefficient. The associated localization scale in momentum is therefore
is the classical diffusion coefficient. The associated localization scale in momentum is therefore 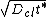 .
.
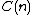 is zero (due to long negative tails), while with the noise a practical approximation is
is zero (due to long negative tails), while with the noise a practical approximation is 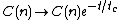 where the coherence time
where the coherence time 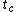 is inversely proportional to the intensity of the noise. Consequently the noise induced diffusion coefficient is
is inversely proportional to the intensity of the noise. Consequently the noise induced diffusion coefficient is
Chaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
and quantum chaos
Quantum chaos
Quantum chaos is a branch of physics which studies how chaotic classical dynamical systems can be described in terms of quantum theory. The primary question that quantum chaos seeks to answer is, "What is the relationship between quantum mechanics and classical chaos?" The correspondence principle...
studies. It describes a particle that is constrained to move on a ring (equivalently: a rotating stick). The particle is kicked periodically by an homogeneous field (equivalently: the gravitation is switched on periodically in short pulses). The model is described by the Hamiltonian
Where
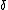 is the Dirac delta function,
is the Dirac delta function,  is the angular position (for example, on a ring), taken modulo
is the angular position (for example, on a ring), taken modulo 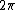 ,
, 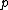 is the momentum, and
is the momentum, and 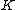 is the kicking strength. Its dynamics are described by the standard map
is the kicking strength. Its dynamics are described by the standard mapWith the caveat that
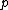 is not periodic, as it is in the standard map. See more details and references on the standard map here, or better in the associated Scholarpedia entry.
is not periodic, as it is in the standard map. See more details and references on the standard map here, or better in the associated Scholarpedia entry.Main properties (classical)
In the classical analysis, if the kicks are strong enough,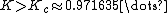 , the system is chaotic and has a positive Maximal Lyapunov exponent (MLE).
, the system is chaotic and has a positive Maximal Lyapunov exponent (MLE).The averaged diffusion of the momentum-squared is a useful parameter in characterizing the delocalization of nearby trajectories. The inductive result of the standard map yields the following equation for momentum
The diffusion can then be calculated by squaring the difference in momentum after the
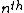 kick and the initial momentum, and then averaging, yielding
kick and the initial momentum, and then averaging, yieldingIn the chaotic domain, the momenta at different time points may be anywhere from entirely uncorrelated to highly correlated. If they are assumed uncorrelated due to the quasi-random behaviour, the sum involving the cross-terms
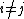 is neglected. In this limit, since the first term is a sum of
is neglected. In this limit, since the first term is a sum of  terms all equalling
terms all equalling 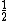 , the momentum diffusion becomes
, the momentum diffusion becomes 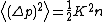 . However, if the momenta at different time points are assumed highly correlated, the sum involving the cross-terms is not neglected, and so it contributes more terms equalling
. However, if the momenta at different time points are assumed highly correlated, the sum involving the cross-terms is not neglected, and so it contributes more terms equalling 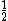 . Altogether, there are
. Altogether, there are 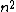 terms to sum, all of the form
terms to sum, all of the form 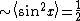 . This gives an upper bound on the momentum diffusion of
. This gives an upper bound on the momentum diffusion of 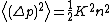 . Therefore, in the chaotic domain, the momentum diffusion is between
. Therefore, in the chaotic domain, the momentum diffusion is betweenThat is, the momentum diffusion in the chaotic domain has somewhere between a linear and a quadratic dependence on the number of kicks. An exact expression for
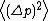 can be obtained in principle by calculating the sums explicitly for an ensemble of trajectories.
can be obtained in principle by calculating the sums explicitly for an ensemble of trajectories.Main properties (quantum)
In the quantum analysis, the Hamiltonian must first be rewritten in operator form, using the substitution to give (in dimensionless form)
to give (in dimensionless form)The wavefunction can then be solved for using Schrödinger's equation
where
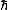 is here scaled according to the period between kicks,
is here scaled according to the period between kicks, 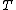 , and the wave-vector of the driving potential,
, and the wave-vector of the driving potential, 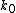 , as
, asThe wavefunction at the
 kick can be expanded in terms of the momentum eigenstates,
kick can be expanded in terms of the momentum eigenstates, 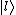 , as
, asIt can be shown that the coefficients are given recursively by
Where
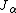 is a Bessel function of order
is a Bessel function of order  .
.Given some set of initial conditions, it is relatively straightforward to numerically solve the recursive equation above for all time, and substitute the calculated coefficients back into the momentum eigenstate decomposition to find the total wavefunction. Squaring this gives the time evolution of the probability distribution, thus providing a complete a quantum mechanical description.
Another way to calculate the time evolution is to iteratively apply the unitary operator
It has been discovered that the classical diffusion is suppressed, and later it has been understood that this is a manifestation of a quantum dynamical localization effect that parallels Anderson localization
Anderson localization
In condensed matter physics, Anderson localization, also known as strong localization, is the absence of diffusion of waves in a disordered medium. This phenomenon is named after the American physicist P. W...
. There is a general argument that leads to the following estimate for the breaktime of the diffusive behavior
Where
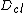 is the classical diffusion coefficient. The associated localization scale in momentum is therefore
is the classical diffusion coefficient. The associated localization scale in momentum is therefore 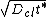 .
.The effect of noise and dissipation
If noise is added to the system, the dynamical localization is destroyed, and diffusion is induced. This is somewhat similar to hopping conductance. The proper analysis requires to figure out how the dynamical correlations that are responsible for the localization effect are diminished. Without the noise the area under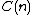 is zero (due to long negative tails), while with the noise a practical approximation is
is zero (due to long negative tails), while with the noise a practical approximation is 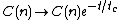 where the coherence time
where the coherence time 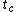 is inversely proportional to the intensity of the noise. Consequently the noise induced diffusion coefficient is
is inversely proportional to the intensity of the noise. Consequently the noise induced diffusion coefficient is-
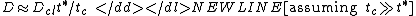
Also the problem of quantum kicked rotator with dissipation (due to coupling to a thermal bath) has been considered. There is an issue here how to introduce an interaction that respects the angle periodicity of the position coordinate, and is still spatially homogeneous. In the first works
coordinate, and is still spatially homogeneous. In the first works
a quantum-optic type interaction has been assumed that involves a momentum dependent coupling. Later a way to formulate a purely position dependent coupling, as in the Calderia-Leggett model, has been figured out, which can be regarded as the earlier version of the DLD model.
Experiments
Experimental realizations of the quantum kicked rotator have been achieved by the Austin group, and by the Auckland group, and have encouraged a renewed interest in the theoretical analysis. In this kind of experiment, a sample of cold atoms provided by a Magneto-optical trapMagneto-optical trapA magneto-optical trap is a device that uses both laser cooling with magneto-optical trapping in order to produce samples of cold, trapped, neutral atoms at temperatures as low as several microkelvins, two or three times the recoil limit.By combining the small momentum of a single photon with a...
interacts with a pulsed standing wave of light. The light being detuned with respect to the atomic transitions, atoms undergo a space-periodic conservative forceConservative forceA conservative force is a force with the property that the work done in moving a particle between two points is independent of the path taken. Equivalently, if a particle travels in a closed loop, the net work done by a conservative force is zero.It is possible to define a numerical value of...
. Hence, the angular dependence is replaced by a dependence on position in the experimental approach. Sub-milliKelvin cooling is necessary to obtain quantum effects: because of the Heisenberg uncertainty principleUncertainty principleIn quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
, the de Broglie wavelength, i.e. the atomic wavelength, can become comparable to the light wavelength. For further information, see.
Thanks to this technique, several phenomena have been investigated, including the noticeable:- quantum Ratchets;
- the Anderson transition in 3D.