Taylor expansions for the moments of functions of random variables
Encyclopedia
In probability theory
, it is possible to approximate the moments
of a function f of a random variable
X using Taylor expansions, provided that f is sufficiently differentiable and that the moments of X are finite. This technique is often used by statisticians
.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, it is possible to approximate the moments
Moment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
of a function f of a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
X using Taylor expansions, provided that f is sufficiently differentiable and that the moments of X are finite. This technique is often used by statisticians
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
.
First moment
-
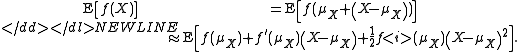
Noting that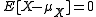
, the 2nd term disappears. Also 
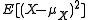is 
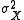. Therefore,
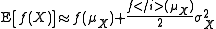
where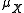
and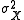 
are the mean and variance of X respectively.
It is possible to generalize this to functions of more than one variable using multivariate Taylor expansions. For example,
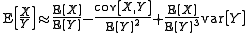
Second moment
Analogously,
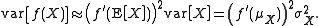
This is a special case of the delta methodDelta methodIn statistics, the delta method is a method for deriving an approximate probability distribution for a function of an asymptotically normal statistical estimator from knowledge of the limiting variance of that estimator...
. For example,
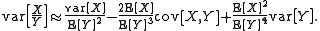
See also
- Propagation of uncertaintyPropagation of uncertaintyIn statistics, propagation of error is the effect of variables' uncertainties on the uncertainty of a function based on them...
- WKB approximationWKB approximationIn mathematical physics, the WKB approximation or WKB method is a method for finding approximate solutions to linear partial differential equations with spatially varying coefficients...
- Propagation of uncertainty