
Taylor-Green vortex
Encyclopedia
In fluid dynamics, the Taylor–Green vortex is a 2-dimensional, unsteady flow of a decaying vortex, which has the exact closed form solution of incompressible Navier-Stokes equations in Cartesian coordinates. It is named after the British physicists and mathematicians Geoffrey Ingram Taylor
and George Green
.
is given by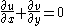
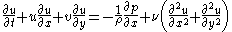
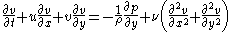
The first of the above equation represents the continuity equation
and the other two represent the momentum equations.
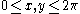 , the solution is given by
, the solution is given by

where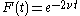 ,
,  being the kinematic viscosity of the fluid. The pressure field
being the kinematic viscosity of the fluid. The pressure field 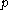 can be obtained by substituting the velocity solution in the momentum equations and is given by
can be obtained by substituting the velocity solution in the momentum equations and is given by
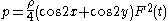
The stream function
of the Taylor–Green vortex solution, i.e. which satisfies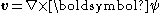 for flow velocity
for flow velocity  , is
, is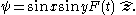
Similarly, the vorticity, which satisfies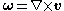 , is given by
, is given by
The Taylor–Green vortex solution may be used for testing and validation of temporal accuracy of Navier-Stokes algorithms.
Geoffrey Ingram Taylor
Sir Geoffrey Ingram Taylor OM was a British physicist, mathematician and expert on fluid dynamics and wave theory. His biographer and one-time student, George Batchelor, described him as "one of the most notable scientists of this century".-Biography:Taylor was born in St. John's Wood, London...
and George Green
George Green
George Green was a British mathematical physicist who wrote An Essay on the Application of Mathematical Analysis to the Theories of Electricity and Magnetism...
.
Incompressible Navier-Stokes equations
The incompressible Navier-Stokes equation in the absence of body forceBody force
A body force is a force that acts throughout the volume of a body, in contrast to contact forces.Gravity and electromagnetic forces are examples of body forces. Centrifugal and Coriolis forces can also be viewed as body forces.This can be put into contrast to the classical definition of surface...
is given by
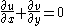
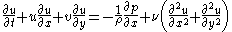
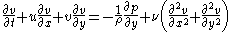
The first of the above equation represents the continuity equation
Continuity equation
A continuity equation in physics is a differential equation that describes the transport of a conserved quantity. Since mass, energy, momentum, electric charge and other natural quantities are conserved under their respective appropriate conditions, a variety of physical phenomena may be described...
and the other two represent the momentum equations.
Taylor-Green vortex solution
In the domain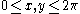 , the solution is given by
, the solution is given by
where
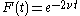 ,
,  being the kinematic viscosity of the fluid. The pressure field
being the kinematic viscosity of the fluid. The pressure field 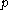 can be obtained by substituting the velocity solution in the momentum equations and is given by
can be obtained by substituting the velocity solution in the momentum equations and is given by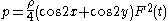
The stream function
Stream function
The stream function is defined for two-dimensional flows of various kinds. The stream function can be used to plot streamlines, which represent the trajectories of particles in a steady flow. Streamlines are perpendicular to equipotential lines...
of the Taylor–Green vortex solution, i.e. which satisfies
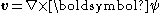 for flow velocity
for flow velocity  , is
, is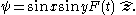
Similarly, the vorticity, which satisfies
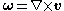 , is given by
, is given by
The Taylor–Green vortex solution may be used for testing and validation of temporal accuracy of Navier-Stokes algorithms.

