
Tate duality
Encyclopedia
In mathematics, Tate duality or Poitou–Tate duality is a duality theorem for Galois cohomology
groups of modules over the Galois group of an algebraic number field or local field
, introduced by and .
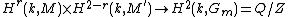
where M is a finite group scheme and M′ its dual Hom(M,Gm).
Galois cohomology
In mathematics, Galois cohomology is the study of the group cohomology of Galois modules, that is, the application of homological algebra to modules for Galois groups...
groups of modules over the Galois group of an algebraic number field or local field
Local field
In mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
, introduced by and .
Local Tate duality
Local Tate duality says there is a perfect pairing of finite groups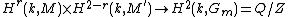
where M is a finite group scheme and M′ its dual Hom(M,Gm).

