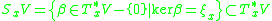Symplectization
Encyclopedia
In mathematics
, the symplectization of a contact manifold is a symplectic manifold
which naturally corresponds to it.
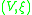 be a contact manifold, and let
be a contact manifold, and let 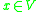 . Consider the set
. Consider the set
of all nonzero 1-forms at , which have the contact plane
, which have the contact plane 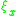 as their kernel. The union
as their kernel. The union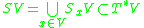
is a symplectic submanifold of the cotangent bundle
of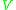 , and thus possesses a natural symplectic structure.
, and thus possesses a natural symplectic structure.
The projection
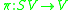 supplies the symplectization with the structure of a principal bundle
supplies the symplectization with the structure of a principal bundle
over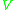 with structure group
with structure group
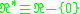 .
.
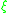 is cooriented by means of a contact form
is cooriented by means of a contact form  , there is another version of symplectization, in which only forms giving the same coorientation to
, there is another version of symplectization, in which only forms giving the same coorientation to 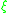 as
as  are considered:
are considered:
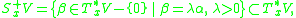
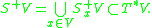
Note that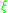 is coorientable if and only if the bundle
is coorientable if and only if the bundle 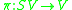 is trivial. Any section
is trivial. Any section
of this bundle is a coorienting form for the contact structure.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the symplectization of a contact manifold is a symplectic manifold
Symplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
which naturally corresponds to it.
Definition
Let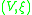 be a contact manifold, and let
be a contact manifold, and let 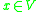 . Consider the set
. Consider the set
of all nonzero 1-forms at
 , which have the contact plane
, which have the contact plane 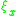 as their kernel. The union
as their kernel. The union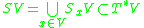
is a symplectic submanifold of the cotangent bundle
Cotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
of
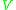 , and thus possesses a natural symplectic structure.
, and thus possesses a natural symplectic structure.The projection
Projection (mathematics)
Generally speaking, in mathematics, a projection is a mapping of a set which is idempotent, which means that a projection is equal to its composition with itself. A projection may also refer to a mapping which has a left inverse. Bot notions are strongly related, as follows...
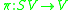 supplies the symplectization with the structure of a principal bundle
supplies the symplectization with the structure of a principal bundlePrincipal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
over
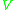 with structure group
with structure groupPrincipal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
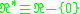 .
.The coorientable case
When the contact structure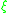 is cooriented by means of a contact form
is cooriented by means of a contact form  , there is another version of symplectization, in which only forms giving the same coorientation to
, there is another version of symplectization, in which only forms giving the same coorientation to 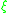 as
as  are considered:
are considered: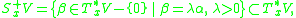
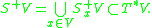
Note that
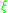 is coorientable if and only if the bundle
is coorientable if and only if the bundle  is trivial. Any section
is trivial. Any sectionSection (fiber bundle)
In the mathematical field of topology, a section of a fiber bundle π is a continuous right inverse of the function π...
of this bundle is a coorienting form for the contact structure.