
Symmetry-preserving filter
Encyclopedia
{context|date=March 2011}
Symmetry-preserving observers, also known as invariant filters, are estimation techniques whose structure and design take advantage of the natural symmetries (or invariances) of the considered nonlinear model. As such, the main benefit is an expected much larger domain of convergence than standard filtering methods, e.g. Extended Kalman Filter (EKF) or Unscented Kalman Filter (UKF).
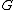 a Lie group, and
a Lie group, and
(local) transformation groups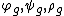 , where
, where 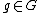 .
.
The nonlinear system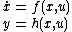
is said to be invariant if it is left unchanged by the action of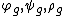 , i.e.
, i.e.
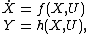
where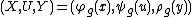 .
.
The system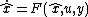 is then an invariant filter if
is then an invariant filter if

where
Given the system and the associated transformation group being considered, there exists a constructive method to determine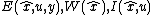 , based on the moving frame method.
, based on the moving frame method.
To analyze the error convergence, an invariant state error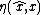 is defined, which is different from the standard output error
is defined, which is different from the standard output error 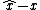 , since the standard output error usually does not preserve the symmetries of the system. One of the main benefit fo symmetry-preserving filters is that the error system is "autonomous", but for the free known invariant vector
, since the standard output error usually does not preserve the symmetries of the system. One of the main benefit fo symmetry-preserving filters is that the error system is "autonomous", but for the free known invariant vector 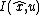 , i.e.
, i.e. 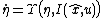 . This important property allows the estimator to have a very large domain of convergence, and to be easy to tune .
. This important property allows the estimator to have a very large domain of convergence, and to be easy to tune .
To choose the gain matrix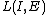 , there are two possibilities:
, there are two possibilities:
Symmetry-preserving observers, also known as invariant filters, are estimation techniques whose structure and design take advantage of the natural symmetries (or invariances) of the considered nonlinear model. As such, the main benefit is an expected much larger domain of convergence than standard filtering methods, e.g. Extended Kalman Filter (EKF) or Unscented Kalman Filter (UKF).
Motivation
Most physical systems possess natural symmetries (or invariance), i.e. there exist transformations (e.g. rotations, translations, scalings) that leave the system unchanged. From mathematical and engineering viewpoints, it makes sense that a filter well-designed for the system being considered should preserve the same invariance properties.Definition
Consider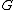 a Lie group, and
a Lie group, and(local) transformation groups
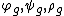 , where
, where 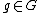 .
.The nonlinear system
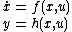
is said to be invariant if it is left unchanged by the action of
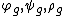 , i.e.
, i.e.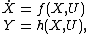
where
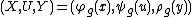 .
.The system
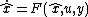 is then an invariant filter if
is then an invariant filter if-
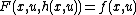 , i.e. that it can be witten
, i.e. that it can be witten 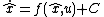 , where the correction term
, where the correction term 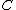 is equal to
is equal to 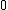 when
when 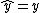
-
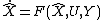 , i.e. it is left unchanged by the transformation group.
, i.e. it is left unchanged by the transformation group.
General equation and main result
It has been proved that every invariant observer reads
where
-
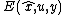 is an invariant output error, which is different to the usual output error
is an invariant output error, which is different to the usual output error 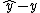
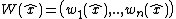 is an invariant frame
is an invariant frame
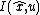 is an invariant vector
is an invariant vector
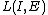 is a freely chosen gain matrix.
is a freely chosen gain matrix.
Given the system and the associated transformation group being considered, there exists a constructive method to determine
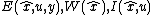 , based on the moving frame method.
, based on the moving frame method.To analyze the error convergence, an invariant state error
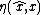 is defined, which is different from the standard output error
is defined, which is different from the standard output error 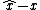 , since the standard output error usually does not preserve the symmetries of the system. One of the main benefit fo symmetry-preserving filters is that the error system is "autonomous", but for the free known invariant vector
, since the standard output error usually does not preserve the symmetries of the system. One of the main benefit fo symmetry-preserving filters is that the error system is "autonomous", but for the free known invariant vector 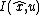 , i.e.
, i.e. 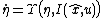 . This important property allows the estimator to have a very large domain of convergence, and to be easy to tune .
. This important property allows the estimator to have a very large domain of convergence, and to be easy to tune .To choose the gain matrix
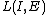 , there are two possibilities:
, there are two possibilities:- a deterministic approach, that leads to the construction of truly nonlinear symmetry-preserving filters (similar to Luenberger-like observers)
- a stochastic approach, that leads to Invariant Extended Kalman FiltersInvariant extended Kalman filterThe invariant extended Kalman filter is a new version of the extended Kalman filter for nonlinear systems possessing symmetries . It combines the advantages of both the EKF and the recently introduced symmetry-preserving filters...
(similar to Kalman-like observers).
Applications
There has been numerous applications that use such invariant observers to estimate the state of the considered system. The application areas include- attitude and heading reference systemsAttitude and Heading Reference SystemsAn attitude heading reference system consists of sensors on three axes that provide heading, attitude and yaw information for aircraft. They are designed to replace traditional mechanical gyroscopic flight instruments and provide superior reliability and accuracy.AHRS consist of either solid-state...
with or without position/velocity sensor (e.g. GPS)
- ground vehicle localization systems
- chemical reactors
- oceanographyOceanographyOceanography , also called oceanology or marine science, is the branch of Earth science that studies the ocean...

